
下列命题:
①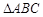 中,若
中,若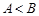 ,则
,则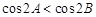 ;
;
②若A,B,C为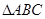 的三个内角,则
的三个内角,则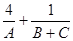 的最小值为
的最小值为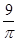
③已知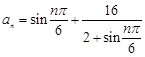
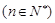 ,则数列
,则数列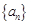 中的最小项为
中的最小项为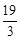 ;
;
④若函数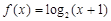 ,且
,且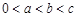 ,则
,则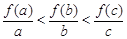 ;
;
⑤函数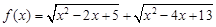 的最小值为
的最小值为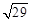 .
.
其中所有正确命题的序号是
②③
解析试题分析:①△ABC中,若A<B,则a<b,由正弦定理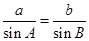
得0<sinA<sinB,又cos2A=1-2sin2A,cos2B=1-2sin2B,
所以cos2A>cos2B,①错误.
②因为A+B+C=π,α=A,β=B+C,α+β=π
所以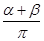 =1,
=1,
原式等价于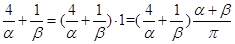
=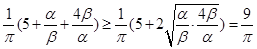 ,
,
当且仅当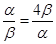 ,即α=2β时取等号.所以②正确.
,即α=2β时取等号.所以②正确.
③因为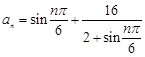 =2+
=2+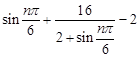 ,因为1≤
,因为1≤ ≤3,
≤3,
所以设t= ,则1≤t≤3.因为函数y=t+
,则1≤t≤3.因为函数y=t+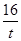 -2在区间(0,4)上单调递减,所以在[1,3]上单调递减,因此,当t=3时,函数有最小值3+
-2在区间(0,4)上单调递减,所以在[1,3]上单调递减,因此,当t=3时,函数有最小值3+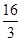 -2=
-2=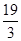 ,则对应数列{an}中的最小项为
,则对应数列{an}中的最小项为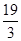 ,所以③正确.
,所以③正确.
④令g(x)=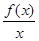 ,则函数g(x)的几何意义为曲线上点与原点连线斜率的大小.由题意可知
,则函数g(x)的几何意义为曲线上点与原点连线斜率的大小.由题意可知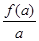 ,
,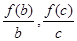 分别看作函数f(x)=log2(x+1)图象上的点(a,f(a)),(b,f(b)),(c,f(b))与原点连线的斜率,由图象可知,
分别看作函数f(x)=log2(x+1)图象上的点(a,f(a)),(b,f(b)),(c,f(b))与原点连线的斜率,由图象可知,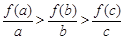 ,所以④错误.
,所以④错误.
⑤因为,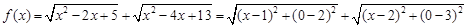 ,问题转化成点P(x,0)到A(1,2),B(2,3)距离之和的最小值。原式等价为|PA|+|PB|的最小值,找出点A关于x轴的对称点D(1,-2).
,问题转化成点P(x,0)到A(1,2),B(2,3)距离之和的最小值。原式等价为|PA|+|PB|的最小值,找出点A关于x轴的对称点D(1,-2).
则|PA|+|PB|=|PD|+|PB|≥|PD|,所以最小值为|PD|=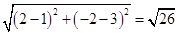 .
.
所以,⑤错误.故答案为:②③.
考点:正弦定理的应用,均值定理的应用,对号函数的性质,对数函数的图象和性质。
点评:难题,本题综合性较强,难度较大。灵活的对问题实施转化,是解题的关键。


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
有一道解三角形的题因纸张破损,有一条件不清,且具体如下:在△ABC中,已知 ,B=
,B=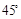 , ,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A=
, ,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A=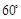 ,请将条件补完整.
,请将条件补完整.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com