
已知函数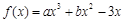
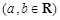 ,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
⑴求函数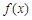 的解析式;
的解析式;
⑵若对于区间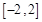 上任意两个自变量的值
上任意两个自变量的值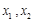 ,都有
,都有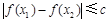 ,求实数
,求实数 的最小值;
的最小值;
⑶若过点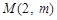
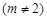 ,可作曲线
,可作曲线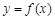 的三条切线,求实数
的三条切线,求实数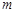 的取值范围.
的取值范围.
⑴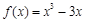 ;⑵
;⑵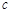 的最小值为
的最小值为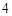 ;⑶
;⑶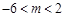 .
.
【解析】
试题分析:⑴ ,由
,由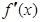 是偶函数得
是偶函数得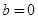 .又
.又 ,所以
,所以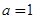 ,由此可得解析式;
,由此可得解析式;
⑵对于区间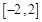 上任意两个自变量的值
上任意两个自变量的值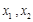 ,都有
,都有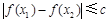 ,则只需
,则只需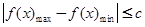 即可.所以接下来就利用导数求
即可.所以接下来就利用导数求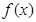 在区间
在区间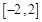 上的最大值与最小值,然后代入
上的最大值与最小值,然后代入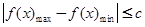 解不等式即可得
解不等式即可得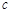 的最小值.⑶易知点
的最小值.⑶易知点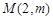
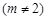 不在曲线
不在曲线 上.凡是过某点的切线(不是在某点处的切线)的问题,都要设出切点坐标然后列方程组..
上.凡是过某点的切线(不是在某点处的切线)的问题,都要设出切点坐标然后列方程组..
设切点为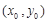 .则
.则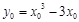 .又
.又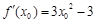 ,∴切线的斜率为
,∴切线的斜率为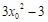 .
.
由此得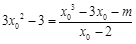 ,即
,即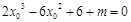 .下面就考查这个方程的解的个数.
.下面就考查这个方程的解的个数.
因为过点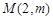
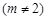 ,可作曲线
,可作曲线 的三条切线,所以方程
的三条切线,所以方程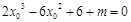 有三个不同的实数解.即函数
有三个不同的实数解.即函数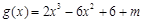 有三个不同的零点.接下来就利用导数结合图象研究这个函数的零点的个数.
有三个不同的零点.接下来就利用导数结合图象研究这个函数的零点的个数.
试题解析:⑴∵ ,1分
,1分
由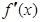 是偶函数得
是偶函数得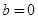 .又
.又 ,所以
,所以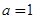 3分
3分
∴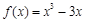 .4分
.4分
⑵令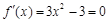 ,即
,即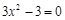 ,解得
,解得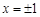 .5分
.5分
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
|
极大值 |
|
极小值 |
|
|
∵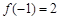 ,
,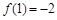 ,
,
∴当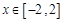 时,
时,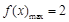 ,
, .6分
.6分
则对于区间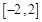 上任意两个自变量的值
上任意两个自变量的值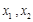 ,都有
,都有
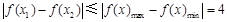 ,所以
,所以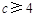 .
.
所以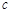 的最小值为
的最小值为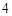 .8分
.8分
⑶∵点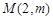
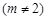 不在曲线
不在曲线 上,
上,
∴设切点为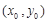 .则
.则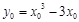 .
.
∵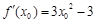 ,∴切线的斜率为
,∴切线的斜率为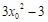 .
.
则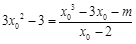 ,即
,即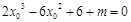 .10分
.10分
因为过点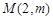
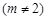 ,可作曲线
,可作曲线 的三条切线,
的三条切线,
所以方程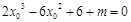 有三个不同的实数解.
有三个不同的实数解.
即函数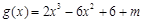 有三个不同的零点.11分
有三个不同的零点.11分
则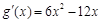 .
.
令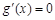 ,解得
,解得
 或
或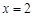 .
.
|
|
|
|
|
|
|
|
|
+ |
|
|
|
+ |
|
|
|
极大值 |
|
极小值 |
|
∴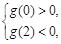 即
即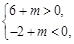 解得
解得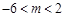 .12分
.12分
考点:1、导数的应用;2、不等关系;3、函数的零点.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011年上海市黄浦区高考数学二模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com