解:(1)∵sinx+cosx=

,∴x不可能是第三象限角,
∴-

<x<0,∴sinx<0,cosx>0,则sinx-cosx<0,
又sinx+cosx=

,平方后得到 1+sin2x=

,
∴sin2x=-

∴(sinx-cosx )
2=1-sin2x=

,
又∵sinx-cosx<0,
∴sinx-cosx=-

.
(2)由于
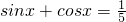
及sinx-cosx=-

.
得:sinx=-

,cosx=

.
∴tanx=-

,
∴
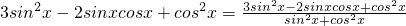
=
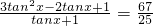
.
分析:(1)由-π<x<0结合条件可知x是第四象限角,从而sinx<0,cosx>0,由此可知sinx-cosx<0.再利用平方关系式求解(sinx-cosx)
2=(sinx+cosx)
2-4sinxcosx)即可求得答案.
(2)利用条件及(1)的结论得到tanx的表达式,再利用sin
2x+cos
2x=1,在表达式的分母增加“1”,然后分子、分母同除cos
2x,得到tanx的表达式,即可求出结果.
点评:本题利用公式(sinx-cosx)
2=(sinx+cosx)
2-4sinxcosx.求解时需要开方,一定要注意正负号的取法,注意角x的范围!本题是基础题,考查三角函数的表达式求值的应用,考查计算能力,注意“1”的代换,以及解题的策略.

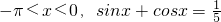 ,求下列各式的值.
,求下列各式的值. ,∴x不可能是第三象限角,
,∴x不可能是第三象限角, <x<0,∴sinx<0,cosx>0,则sinx-cosx<0,
<x<0,∴sinx<0,cosx>0,则sinx-cosx<0, ,平方后得到 1+sin2x=
,平方后得到 1+sin2x= ,
, ∴(sinx-cosx )2=1-sin2x=
∴(sinx-cosx )2=1-sin2x= ,
, .
.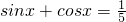 及sinx-cosx=-
及sinx-cosx=- .
. ,cosx=
,cosx= .
. ,
,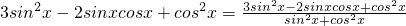
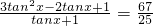 .
.
