
如下图,已知△OFQ的面积为S,且![]() ·
·![]() =1,
=1,
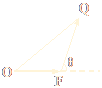
(1)若S的范围为![]() <S<2,求向量
<S<2,求向量![]() 与
与![]() 的夹角θ的取值范围;
的夹角θ的取值范围;
(2)设|![]() |=c(c≥2),S=
|=c(c≥2),S=![]() c,若以O为中心,F为焦点的椭圆经过点Q,当|
c,若以O为中心,F为焦点的椭圆经过点Q,当|![]() |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.
(1) ![]() <θ<arctan4.
<θ<arctan4.
 (2) 椭圆方程为
(2) 椭圆方程为![]() .
.
本题考查向量的基本知识、三角知识及最值问题在解析几何中的综合运用.
(1)∵![]() ·
·![]() =1,∴|
=1,∴|![]() |·|
|·|![]() |·cosθ=1.
|·cosθ=1.
又![]() |
|![]() |·|
|·|![]() |·sin(180°-θ)=S,
|·sin(180°-θ)=S,
∴tanθ=2S,S=![]() .
.
又![]() <S<2,∴
<S<2,∴![]() <
<![]() <2,即1<tanθ<4,
<2,即1<tanθ<4,
∴![]() <θ<arctan4.
<θ<arctan4.
(2)以![]() 所在的直线为x轴,以
所在的直线为x轴,以![]() 的过O点的垂线为y轴建立直角坐标系(如下图).
的过O点的垂线为y轴建立直角坐标系(如下图).

∴O(0,0),F(c,0),Q(x0,y0).
设椭圆方程为![]() +
+![]() =1.
=1.
又![]() ·
·![]() =1,S=
=1,S=![]() c,
c,
∴(c,0)·(x0-c,y0)=1. ①
![]() ·c·|y0|=
·c·|y0|=![]() c. ②
c. ②
由①得c(x0-c)=1![]() x0=c+
x0=c+![]() .
.
由②得|y0|=![]() .
.
∴|![]() |=
|=![]() =
=![]() .
.
∵c≥2,
∴当c=2时,|![]() |min=
|min=![]() =
=![]() ,
,
此时Q(![]() ,±
,±![]() ),F(2,0).
),F(2,0).
代入椭圆方程得
∴a2=10,b2=6.
∴椭圆方程为![]() .
.
评析:新知识(向量)在几何中的应用是值得关注的趋势.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:资阳市2005-2006学年度高中二年级第一学期期末质量检测理科数学 题型:044
如下图,已知△OFQ的面积为S,且![]() ·
·![]() =1,
=1,

(Ⅰ)若S满足条件![]() <S<2,求向量
<S<2,求向量![]() 与
与![]() 的夹角θ的取值范围;
的夹角θ的取值范围;
(Ⅱ)设|![]() |=c(c≥2),S=
|=c(c≥2),S=![]() c,若以O为中心,F为焦点的椭圆经过点Q,当|
c,若以O为中心,F为焦点的椭圆经过点Q,当|![]() |取得最小值时,求此椭圆的方程.
|取得最小值时,求此椭圆的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com