练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    设I={1,2,3,…,9},已知(1)( A)∩B={3,7},(2)( B)∩A={2,8},(3)( A)∩(B)={1,5,6},求集合A和B.

    思路分析:通常的题目是首先给出集合,然后求集合的交、并、补等运算结果.本题恰恰相反,先给出了集合A、B的运算结果,然后要求求集合A、B.可以借助Venn图把相关运算的结果表示出来,自然地就得出集合A、B了.

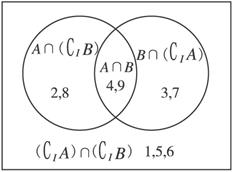
                          图1-1-6

    解:用Venn图表示集合I、A、B的关系,如图1-1-6所示的有关区域分别表示集合A∩B,(A)∩B,A∩(B),(A)∩(B),并填上相应的元素,可得A={2,4,8,9},B={3,4,7,9}.

    评述:①当集合中元素的个数有限或要判断两集合相互之间的关系时,常可借助于Venn图,以形助数.

    ②在图1-1-6中,根据集合的意义,能得到(M∪N)=(M)∩(N),  (M∩N)=( M)∪(N)(德·摩根律).


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设集合I={1,2,3,4,5},选择I的两个非空子集A和B，要使B中最小的数大于A中最大的数，则不同的选择方法共有__________________种.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设F是椭圆+=1的右焦点，且椭圆上至少有21个不同的点Pi(i=1,2,3,…)，使|FP1|,|FP2|,|FP3|，…组成公差为d的等差数列，则d的取值范围为_______.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设平面向量a1,a2,a3的和a1+a2+a3=0,如果平面向量b1,b2,b3满足|bi|=2|ai|,且ai顺时针旋转30°后与bi同向,其中i=1,2,3,则(    )

    A.-b1+b2+b3=0                     B.b1-b2+b3=0

    C.b1+b2-b3=0                      D.b1+b2+b3=0

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知A={a1，a2，a3，a4，a5},B={a12，a22，a32，a42，a52}, ai∈N（i=1,2,3,4,5）

    设a1<a2<a3<a4<a5且A∩B={a1,a4}，a1+a4=10，又A∪B元素之和为224，

    求：（1）a1 ，a4  （2）A

    查看答案和解析>>

    同步练习册答案