
| |||||||||||||||||||
(1) |
解析:如图所示,取棱锥底面中心O,则AC∩BD=O.连结SO,则SO⊥平面AC,∠SBO为SB与底面AC所成角.在Rt△SBO中,SB=SA=a,BO=
|
(2) |
取BC中点F,连结FO、SF,∵△BSC为等边三角形,∴SF⊥BC. ∵SO⊥底面AC,∴FO⊥BC(三垂线定理的逆定理). ∴∠SFO为侧面SBC与底面AC所成角. 在Rt△SFO中,OF= ∴tan∠SFO= |
(3) |
过C作CE⊥SD于E,连结AE. ∵正四棱锥S-ABCD侧面是全等的正三角形,∴AE⊥SD且AE=CE,∠AEC为相邻两侧面SCD与SDA所成二面角的平面角. 在△AEC中,AC= ∴cos∠AFC= ∴相邻两侧面SCD与SDA所成的二面角为(π-arccos |
(4) |
延长FO交AD于G,则G为AD的中点.SG⊥AD,SG=SF= 平面SBC与平面SDA有公共点S,它们所成二面角的棱l过点S. ∵BC∥AD,AD ∵SF⊥BC,SG⊥AD,BC∥AD,∴SF⊥l,SG⊥l,∴∠FSG为所求二面角的平面角. 在△SFG中,SF=SG= ∴相对两侧面SBC与SAD所成角为arccos 点评:(1)研究二面角问题,关键是抓平面角.作二面角的平面角常有下列三种方法:①用定义;②作二面角棱的垂面,利用三垂线定理;③利用公式cosθ= (2)如果两个面的交线没有给出,如何找交线的问题也是高考常考内容.找交线的方法常用公理2或线面平行的性质定理. |


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源:2015届山东省高一上学期期末模拟数学试卷(解析版) 题型:选择题
如图所示,在正四棱锥S-ABCD中,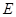 是
是 的中点,P点在侧面△SCD内及其边界上运动,并且总是保持
的中点,P点在侧面△SCD内及其边界上运动,并且总是保持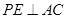 .则动点
.则动点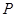 的轨迹与△
的轨迹与△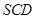 组成的相关图形最有可有是图中的( )
组成的相关图形最有可有是图中的( )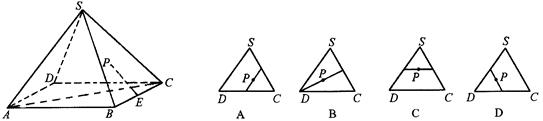
查看答案和解析>>
科目:高中数学 来源:2014届辽宁省高一上学期12月月考考试数学 题型:选择题
如图所示,在正四棱锥S-ABCD中,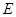 是
是 的中点,P点在侧面△SCD内及其边界
的中点,P点在侧面△SCD内及其边界
上运动,并且总是保持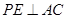 .则动点
.则动点 的轨迹与△
的轨迹与△ 组成的相关图形最有可有
组成的相关图形最有可有
是图中的 ( )
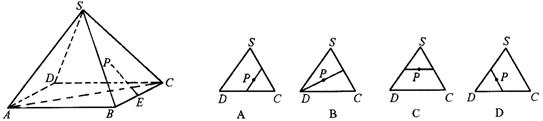
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com