练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{25}$=1的渐近线方程是（　　）
    A．y=$±\frac{5}{4}$xB．y=$±\frac{4}{5}$xC．y=$±\frac{16}{25}$xD．y=±$\frac{25}{16}$x

    分析 根据双曲线的方程求得渐近线方程为y=±$\frac{b}{a}$x，即可求出，

    解答 解：双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{25}$=1中a=4，b=5，
    故其渐近线方程是y=±$\frac{5}{4}$x，
    故选：A．

    点评 本题考查双曲线的标准方程，以及双曲线的简单性质的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    14．已知m．n是空间两条不同的直线，α是一个平面，则下列命题为假命题的是（　　）
    A．m⊥α，n∥α⇒m⊥nB．m⊥α，n⊥α⇒m∥n
    C．m⊥α，n⊥m⇒n∥α或n?αD．m∥α，n⊥m⇒n⊥α或n∥α或n?α

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．函数y=cos2x，x∈R的最小正周期为（　　）
    A．2B．πC．2πD．$\frac{1}{π}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．某次考试，班主任从全班同学中随机抽取一个容量为8的样本，他们的数学、物理分数对应如下表：
    学生编号12345678
    数学分数x6065707580859095
    物理分数y7277808488909395
    绘出散点图如下：

    根据以上信息，判断下列结论：
    ①根据此散点图，可以判断数学成绩与物理成绩具有线性相关关系；
    ②根据此散点图，可以判断数学成绩与物理成绩具有一次函数关系；
    ③甲同学数学考了80分，那么，他的物理成绩一定比数学只考了60分的乙同学的物理成绩要高．
    其中正确的个数为（　　）
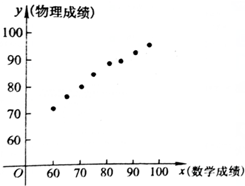
    A．0B．3C．2D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．已知向量$\overrightarrow{a}$=（5，2），$\overrightarrow{b}$=（1，6），则$\overrightarrow{a}$+$\overrightarrow{b}$的坐标为（　　）
    A．（4，-4）B．（6，8）C．（5，12）D．（3，11）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．将函数y=sin2x的图象向左平移$\frac{π}{3}$个单位长度，所得图象的函数解析式为（　　）
    A．y=sin（2x+$\frac{π}{3}$）B．y=sin（2x-$\frac{π}{3}$）C．y=sin（2x+$\frac{2π}{3}$）D．y=sin（2x+$\frac{π}{6}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知函数f（x）=x3-x+3，则曲线y=f（x）在点（1，f（1））处的切线方程为（　　）
    A．2x-y+1=0B．x-2y+1=0C．2x+y+1=0D．2x-y+2=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知正四面体ABCD中，E是AB的中点，则异面直线CE与BD所成角的余弦值为（　　）
    A．$\frac{\sqrt{3}}{6}$B．$\frac{\sqrt{6}}{3}$C．$\frac{\sqrt{2}}{2}$D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

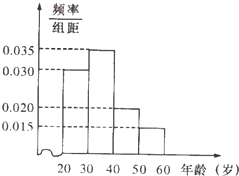    16．某工厂有120名工人，其年龄都在20～60岁之间，各年龄段人数按[20，30），[30，40），[40，50），[50，60）分成四组，其频率分布直方图如图所示．工厂为了开发新产品，引进了新的生产设备，要求每个工人都要参加A、B两项培训，培训结束后进行结业考试．已知各年龄段两项培训结业考试成绩优秀的人数如表所示．假设两项培训是相互独立的，结业考试也互不影响．
     年龄分组 A项培训成绩优秀人数 B项培训成绩优秀人数
    [20，30） 27 16
    [30，40） 28 18
    [40，50） 26 9
    [50，60] 6 4
    （1）若用分层抽样法从全厂工人中抽取一个容量为40的样本，求四个年龄段应分别抽取的人数；
    （2）根据频率分布直方图，估计全厂工人的平均年龄；
    （3）随机从年龄段[20，30）和[40，50）中各抽取1人，设这两人中AB两项培训结业考试成绩都优秀的人数为X，求X的分布列和数学期望．

    查看答案和解析>>

    同步练习册答案