
如图, 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 的切线,
的切线, 与
与 的延长线交于点
的延长线交于点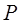 ,
, 为切点.若
为切点.若 ,
, ,
, 的平分线
的平分线 与
与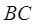 和⊙
和⊙ 分别交于点
分别交于点 、
、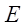 ,求
,求 的值。
的值。

科目:高中数学 来源: 题型:
 如图,是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面PBC.
如图,是⊙O的直径,点C是⊙O上的动点,PA垂直于⊙O所在的平面PBC.| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 注意:在以下(1)(2)两题中任选一题.如果两题都做,按(1)给分.
注意:在以下(1)(2)两题中任选一题.如果两题都做,按(1)给分.| π |
| 6 |
| 5π |
| 6 |
| 19 |
| 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•郑州二模)选修4-1:平面几何
(2012•郑州二模)选修4-1:平面几何| 3 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三5月高考三轮模拟文科数学试卷(解析版) 题型:解答题
如图, 是半圆
是半圆 的直径,
的直径, 是半圆
是半圆 上除
上除 、
、 外的一个动点,
外的一个动点, 平面
平面 ,
, ,
, ,
, ,
, .
.

⑴证明:平面 平面
平面 ;
;
⑵试探究当 在什么位置时三棱锥
在什么位置时三棱锥 的体积取得最大值,请说明理由并求出这个最大值.
的体积取得最大值,请说明理由并求出这个最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com