
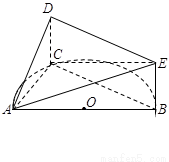
如图, 是半圆
是半圆 的直径,
的直径, 是半圆
是半圆 上除
上除 、
、 外的一个动点,
外的一个动点, 平面
平面 ,
, ,
, ,
, ,
, .
.

⑴证明:平面 平面
平面 ;
;
⑵试探究当 在什么位置时三棱锥
在什么位置时三棱锥 的体积取得最大值,请说明理由并求出这个最大值.
的体积取得最大值,请说明理由并求出这个最大值.
⑴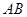 是直径,所以
是直径,所以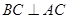 ,因为
,因为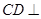 平面
平面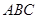 ,
,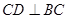 ,所以
,所以 平面
平面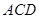 因为
因为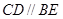 ,又因为
,又因为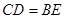 ,所以
,所以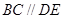 ,所以
,所以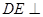 平面ACD,因为
平面ACD,因为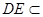 平面
平面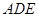 ,所以平面
,所以平面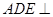 平面
平面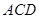
⑵当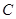 为半圆弧中点时三棱锥
为半圆弧中点时三棱锥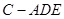 的体积取得最大值,最大值为
的体积取得最大值,最大值为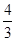
【解析】
试题分析:⑴因为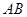 是直径,所以
是直径,所以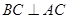 ,因为
,因为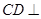 平面
平面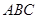 ,
,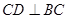 ,因为
,因为 ,所以
,所以 平面
平面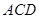
因为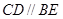 ,又因为
,又因为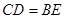 ,所以四边形
,所以四边形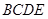 是平行四边形,所以
是平行四边形,所以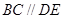 ,所以
,所以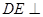 平面,因为
平面,因为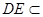 平面
平面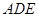 ,所以平面
,所以平面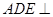 平面
平面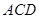
⑵依题意,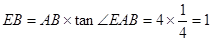 ,
,
由⑴知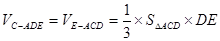
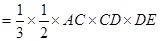 ,
,
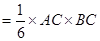 ,
,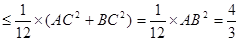 ,等号当且仅当
,等号当且仅当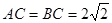 时成立,所以当
时成立,所以当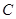 为半圆弧中点时三棱锥
为半圆弧中点时三棱锥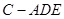 的
的
体积取得最大值,最大值为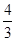
(备注:此时,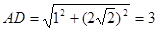 ,
,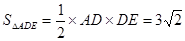 ,设三棱锥
,设三棱锥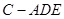 的高为
的高为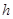 ,则
,则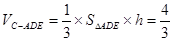 ,
,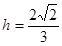 ).
).
考点:线面垂直的判定与性质及椎体体积
点评:第一问要证明两面垂直只需证明其中一个平面内的一条直线垂直于另外一面,即转化为证明线面垂直;第二问首先采用等体积法将所求椎体的体积转化求解的角度,而后借助于均值不等式求得最大值


科目:高中数学 来源:2012-2013学年陕西西安高三第十二次适应性训练文数学卷(解析版) 题型:填空题
如图,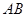 是半圆
是半圆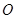 的直径,点
的直径,点 在半圆上,
在半圆上,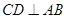 ,垂足为
,垂足为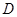 ,且
,且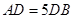 ,设
,设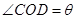 ,则
,则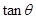 的值为 _________;
的值为 _________;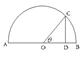
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三5月高考三轮模拟理科数学试卷(解析版) 题型:解答题
如图,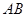 是半圆
是半圆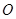 的直径,
的直径,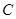 是半圆
是半圆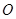 上除
上除 、
、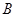 外的一个动点,
外的一个动点, 垂直于半圆
垂直于半圆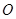 所在的平面,
所在的平面,  ∥
∥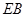 ,
,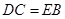 ,
,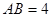 ,
, .
.
⑴证明:平面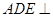 平面
平面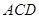 ;
;
⑵当三棱锥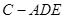 体积最大时,求二面角
体积最大时,求二面角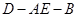 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年深圳市高三第一次调研考试数学文卷 题型:填空题
(二)选做题:第14、15题为选做题,考生只能选做一题,两题全答的,只计算第一题的得分.
(坐标系与参数方程)在极坐标系中, 是曲线
是曲线
 上任意两点,则线段
上任意两点,则线段 长度的最大值为
.
长度的最大值为
.
 (几何证明选讲)如图,
(几何证明选讲)如图,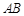 是半圆
是半圆 的直径,
的直径, 是半圆
是半圆 上异于
上异于 的点,
的点, ,垂足为
,垂足为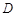 ,已知
,已知 ,
,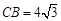 ,则
,则 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省中山市高三第一次月考数学理卷 题型:填空题
(二)选做题(14~15题,考生只能从中选做一题)
(几何证明选讲选做题)如图5, 是半圆
是半圆 的直径,点
的直径,点 在
在
半圆上, ,垂足为
,垂足为 ,且
,且 ,设
,设 ,
,
则 的值为 .
的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com