
已知数列{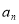 }中,
}中,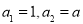 ,且
,且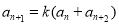 对任意正整数都成立,数列{
对任意正整数都成立,数列{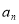 }的前n项和为Sn。
}的前n项和为Sn。
(1)若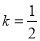 ,且
,且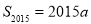 ,求a;
,求a;
(2)是否存在实数k,使数列{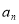 }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项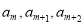 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若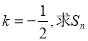 。
。
(1)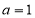 (2)
(2)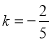 (3)
(3)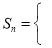


【解析】
试题分析:(1)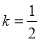 时,
时,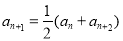 ,由等差数列定义知数列
,由等差数列定义知数列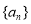 是等差数列,由
是等差数列,由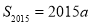 可得
可得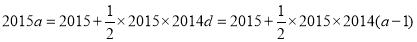 ,解得
,解得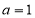 ,(2)等差数列与等比数列的综合,从等差数列列等量关系:因为数列{
,(2)等差数列与等比数列的综合,从等差数列列等量关系:因为数列{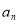 }是公比不为1,所以
}是公比不为1,所以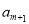 不为等差中项,只需讨论
不为等差中项,只需讨论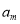 与
与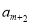 为等差中项:若
为等差中项:若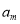 为等差中项,则
为等差中项,则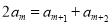 ,即
,即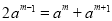 ,化简得:
,化简得: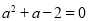 ,解得
,解得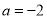 (舍1);
(舍1);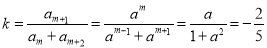 ;同理若
;同理若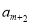 为等差中项,
为等差中项,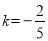 (3)
(3)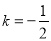 则
则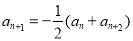 ,
,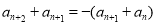 ,从而
,从而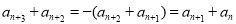 ,所以求和时要重新组合,每两项作为一组,先求
,所以求和时要重新组合,每两项作为一组,先求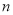 是偶数时,
是偶数时,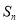
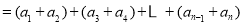
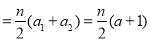 ,再求
,再求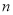 是奇数时,
是奇数时,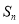
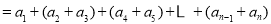
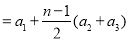
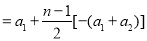
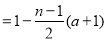 ,
,
试题解析:(1)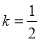 时,
时,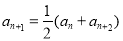 ,
,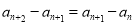 ,所以数列
,所以数列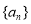 是等差数列 1分
是等差数列 1分
此时首项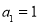 ,公差
,公差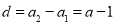 ,数列
,数列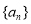 的前
的前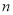 项和是
项和是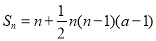 3分
3分
故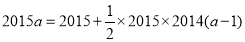 ,即
,即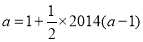 ,得
,得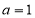 ; 4分
; 4分
(没有过程,直接写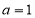 不给分)
不给分)
(2)设数列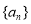 是等比数列,则它的公比
是等比数列,则它的公比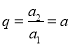 ,所以
,所以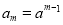 ,
,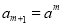 ,
,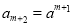 6分
6分
①若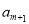 为等差中项,则
为等差中项,则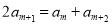 ,即
,即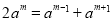 ,解得:
,解得: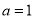 ,不合题意;
,不合题意;
②若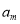 为等差中项,则
为等差中项,则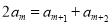 ,即
,即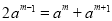 ,化简得:
,化简得: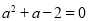 ,
,
解得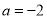 (舍1);
(舍1);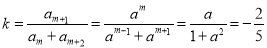 ;
;
③若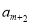 为等差中项,则
为等差中项,则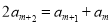 ,即
,即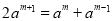 ,化简得:
,化简得: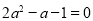 ,
,
解得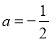 ;
;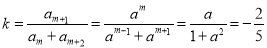 ; 9分
; 9分
综上可得,满足要求的实数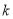 有且仅有一个,
有且仅有一个,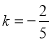 ; 10分
; 10分
(3)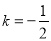 则
则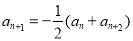 ,
,
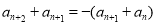 ,
,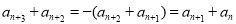 , 12分
, 12分
当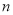 是偶数时,
是偶数时,
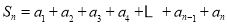
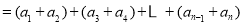
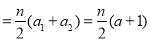 ,
,
当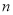 是奇数时,
是奇数时,
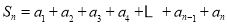
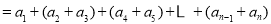
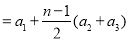
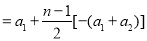
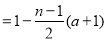 ,
,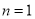 也适合上式, 15分
也适合上式, 15分
综上可得,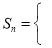

 . 16分
. 16分
考点:等差数列与等比数列
考点分析: 考点1:等比数列 试题属性

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年辽宁省沈阳市三年级教学质量监测一理科数学试卷(解析版) 题型:选择题
函数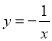 的图象按向量
的图象按向量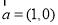 平移之后得到的函数图象与函数
平移之后得到的函数图象与函数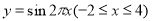 的图象所有交点的橫坐标之和等于( )
的图象所有交点的橫坐标之和等于( )
A.2 B.4 C. 6 D. 8
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省扬州市高三上学期期末文科数学试卷(解析版) 题型:填空题
已知A(0,1),曲线C:y=logax恒过点B,若P是曲线C上的动点,且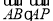 的最小值为2,则a=
的最小值为2,则a=
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省高二上学期期末考试数学试卷(解析版) 题型:选择题
已知点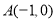 ,
,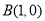 ,
,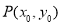 是直线
是直线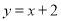 上任意一点,以
上任意一点,以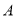 ,
,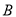 为焦点的椭圆过
为焦点的椭圆过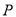 ,记椭圆离心率
,记椭圆离心率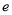 关于
关于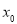 的函数为
的函数为 ,那么下列结论正确的是( )
,那么下列结论正确的是( )
A. 与
与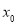 一 一对应 B.函数
一 一对应 B.函数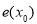 无最小值,有最大值
无最小值,有最大值
C.函数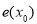 是增函数 D.函数
是增函数 D.函数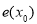 有最小值,无最大值
有最小值,无最大值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com