Question

函数y=8x²-lnx的单调减区间是________，极小值是________．

Answer 1

（0，）    
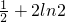
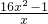
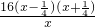
分析：先求出其导函数f'（x）=16x-==，利用导函数值的正负来求其单调区间，进而求得其极值．（注意是在定义域内研究其单调性）
解答：因为y=f（x）=8x²-lnx，
∴f'（x）=16x-==
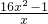
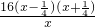
∵x＞0
∴当x＞时，f'（x）＞0，即f（x）递增；
当0＜x＜时，f'（x）＜0，f（x）递减．
且f（x） 极小值为f（）=8×-ln=+2ln2．
故答案为：（0，），+2ln2．
点评：本题主要考查利用导数研究函数的极值以及函数的单调性，利用导数研究函数的单调性，求解函数的单调区间、极值、最值问题，是函数这一章最基本的知识，也是教学中的重点和难点，学生应熟练掌握．