
【题目】近年来,我国电子商务行业迎来了蓬勃发展的新机遇,但是电子商务行业由于缺乏监管,服务质量有待提高.某部门为了对本地的电商行业进行有效监管,调查了甲、乙两家电商的某种同类产品连续十天的销售额(单位:万元),得到如下茎叶图:
甲 | 乙 | |||||
7 | 5 | 10 | 7 | |||
9 | 5 | 3 | 11 | 5 | 7 | 8 |
8 | 6 | 12 | 3 | 5 | ||
4 | 2 | 13 | 2 | 6 | 9 | |
1 | 14 | 8 | ||||
(1)根据茎叶图判断甲、乙两家电商对这种产品的销售谁更稳定些?
(2)为了综合评估本地电商的销售情况,从甲、乙两家电商十天的销售数据中各抽取两天的销售数据,其中销售额不低于120万元的天数分别记为![]() ,令
,令![]() ,求随机变量Y的分布列和数学期望.
,求随机变量Y的分布列和数学期望.
【答案】甲电商对这种产品的销售谁更稳定. (2) 分布列见解析,数学期望为![]() .
.
【解析】
(1)先分别求出甲、乙电商连续十天的销售额的平均数,再求出其方差,从而作出判断.
(2)根据意义甲电商对这种产品的销售额不低于120万元的天数有5天,乙电商对这种产品的销售额不低于120万元的天数有6天. ![]() 的所有可能取值为0,1,2,
的所有可能取值为0,1,2,![]() 的所有可能取值为0,1,2,由
的所有可能取值为0,1,2,由![]() ,所以随机变量Y的所有可能取值为0,1,2,3,4,然后分别求出概率得出分布列求出期望.
,所以随机变量Y的所有可能取值为0,1,2,3,4,然后分别求出概率得出分布列求出期望.
(1) 设甲、乙电商连续十天的销售额的平均数分别为![]() ,方差分别为
,方差分别为![]()
![]() (万元)
(万元)
![]()
![]()
![]()
![]() (万元)
(万元)
![]()
![]()
![]()
由![]() ,所以甲电商对这种产品的销售谁更稳定.
,所以甲电商对这种产品的销售谁更稳定.
(2)由题意![]() 的所有可能取值为0,1,2,
的所有可能取值为0,1,2,![]() 的所有可能取值为0,1,2,
的所有可能取值为0,1,2,
由![]() ,所以随机变量Y的所有可能取值为0,1,2,3,4
,所以随机变量Y的所有可能取值为0,1,2,3,4
其中甲电商对这种产品的销售额不低于120万元的天数有5天.
乙电商对这种产品的销售额不低于120万元的天数有6天.
![]()
![]()
![]()
![]()
![]()
则随机变量Y的分布列为
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
则随机变量Y的数学期望为![]()


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数) 上任意一点
为参数) 上任意一点![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点
.以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 为正项等比数列,
为正项等比数列,![]() 为
为![]() 的前
的前![]() 项和,若
项和,若![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)从三个条件:①![]() ;②
;②![]() ;③
;③![]() 中任选一个作为已知条件,求数列
中任选一个作为已知条件,求数列![]() 的前
的前![]() 项和
项和![]() .
.
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右顶点分别为C、D,且过点
的左、右顶点分别为C、D,且过点![]() ,P是椭圆上异于C、D的任意一点,直线PC,PD的斜率之积为
,P是椭圆上异于C、D的任意一点,直线PC,PD的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)O为坐标原点,设直线CP交定直线x = m于点M,当m为何值时,![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在全民抗击新冠肺炎疫情期间,北京市开展了“停课不停学”活动,此活动为学生提供了多种网络课程资源以供选择使用.活动开展一个月后,某学校随机抽取了高三年级的甲、乙两个班级进行网络问卷调查,统计学生每天的学习时间,将样本数据分成![]() 五组,并整理得到如下频率分布直方图:
五组,并整理得到如下频率分布直方图:
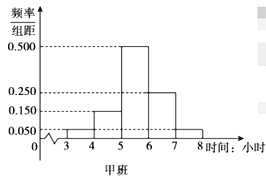
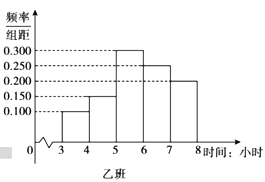
(1)已知该校高三年级共有600名学生,根据甲班的统计数据,估计该校高三年级每天学习时间达到5小时及以上的学生人数;
(2)已知这两个班级各有40名学生,从甲、乙两个班级每天学习时间不足4小时的学生中随机抽取3人,记从甲班抽到的学生人数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)记甲、乙两个班级学生每天学习时间的方差分别为![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 在区间
在区间![]() 单调递增,下述三个结论:①
单调递增,下述三个结论:①![]() 的取值范围是
的取值范围是![]() ;②
;②![]() 在
在![]() 存在零点;③
存在零点;③![]() 在
在![]() 至多有4个极值点.其中所有正确结论的编号是( )
至多有4个极值点.其中所有正确结论的编号是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 的底面
的底面![]() 为平行四边形,
为平行四边形,![]() 底面
底面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
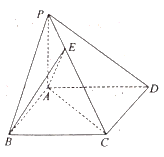
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)在侧棱![]() 上是否存在点E,使
上是否存在点E,使![]() 与底面
与底面![]() 所成的角为45°?若存在,求
所成的角为45°?若存在,求![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com