
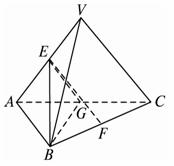
(1)求证:EF是VA与BC的公垂线;
(2)求VA与BC的距离;
(3)求VC与BE所成角的大小;
(4)VF与BE所成角的大小.
解析:(1)连结VF、AF.?
∵△ABC≌△VBC,∴AF=VF.?
又E 为VA的中点,?
∴EF⊥VA.?
同理可得EF⊥BC.?
∴EF是VA与BC的公垂线.?
(2)∵EF是VA与BC的公垂线,?
∴EF的长即为VA与BC的距离.?
由所有的棱长均为a,求得AF=VF=![]() .?
.?
进而可得EF =![]() . ∴VA与BC的距离为
. ∴VA与BC的距离为![]() .?
.?
(3)∵E为VA的中点,?
∴取AC的中点G,连结EG、BG.则EG∥VC.?
∴∠BEG或其补角即为VC与BE所成的角.?

在△BEG中,BE=BG=![]() ,EG=
,EG=![]() .?
.?
由余弦定理可得 cos∠BEG=![]() .?
.?
∴VC与BE所成的角为arccos![]() .?
.?
(4)∵E为VA的中点,?
∴取AF的中点M,连结EM、BM,则EM∥VF.?
∴∠BEM或其补角即为VF与BE所成的角.?
在△BEM中,BE=![]() ,EM=
,EM=![]() .?
.?
而BM=MF2+BF2=![]() .?
.?
由余弦定理得cos∠BEM =![]() .?
.?
∴VF与BE所成的角为arccos![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
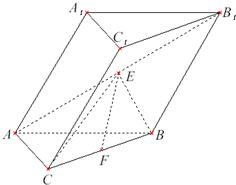 如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.
如图,在斜三棱柱ABC-A1B1C1中,AC=BC,AC⊥BC.侧面A1ABB1是边长为a的菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点. | 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图△ABC中,AC=BC=
如图△ABC中,AC=BC=
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源:设计必修一数学(人教A版) 人教A版 题型:022
如图,有一块边长为a的正方形铁皮,将其四个角各截去一个边长为x的小正方形,然后折成一个无盖的盒子,写出体积V以x为自变量的函数式是________,这个函数的定义域为________.

查看答案和解析>>
科目:高中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com