
【题目】已知椭圆 ![]() 的左顶点和上顶点分别为A、B,左、右焦点分别是F1 , F2 , 在线段AB上有且只有一个点P满足PF1⊥PF2 , 则椭圆的离心率为( )
的左顶点和上顶点分别为A、B,左、右焦点分别是F1 , F2 , 在线段AB上有且只有一个点P满足PF1⊥PF2 , 则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】D
【解析】解:依题意,作图如下: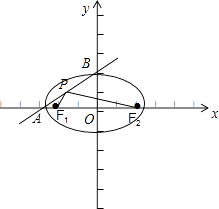
由A(﹣a,0),B(0,b),F1(﹣c,0),F2(c,0),
可得直线AB的方程为: ![]() +
+ ![]() =1,整理得:bx﹣ay+ab=0,
=1,整理得:bx﹣ay+ab=0,
设直线AB上的点P(x,y),则bx=ay﹣ab,
x= ![]() y﹣a,
y﹣a,
由PF1⊥PF2 ,
∴ ![]()
![]() =(﹣c﹣x,﹣y)(c﹣x,﹣y)=x2+y2﹣c2
=(﹣c﹣x,﹣y)(c﹣x,﹣y)=x2+y2﹣c2
=( ![]() y﹣a)2+y2﹣c2 ,
y﹣a)2+y2﹣c2 ,
令f(y)=( ![]() y﹣a)2+y2﹣c2 ,
y﹣a)2+y2﹣c2 ,
则f′(y)=2( ![]() y﹣a)
y﹣a) ![]() +2y,
+2y,
由f′(y)=0得:y= ![]() ,于是x=﹣
,于是x=﹣ ![]() ,
,
∴ ![]()
![]() =(﹣
=(﹣ ![]() )2+(
)2+( ![]() )2﹣c2=0,
)2﹣c2=0,
整理得: ![]() =c2 , 又b2=a2﹣c2 , e2=
=c2 , 又b2=a2﹣c2 , e2= ![]() ,
,
∴e4﹣3e2+1=0,
∴e2= ![]() ,又椭圆的离心率e∈(0,1),
,又椭圆的离心率e∈(0,1),
∴e2= ![]() =(
=( ![]() )2 ,
)2 ,
可得e= ![]() ,
,
故选:D.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】若Ai(i=1,2,3,…,n)是△AOB所在平面内的点,且 ![]()
![]() =
= ![]()
![]() ,给出下列说法:
,给出下列说法:
·(1)| ![]() |=|
|=| ![]() |=|
|=| ![]() |=…=|
|=…=| ![]() |
|
·(2)| ![]() |的最小值一定是|
|的最小值一定是| ![]() |
|
·(3)点A和点Ai一定共线
·(4)向量 ![]() 及
及 ![]() 在向量
在向量 ![]() 方向上的投影必定相等
方向上的投影必定相等
其中正确的个数是( )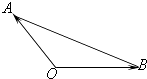
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设CD=2x,梯形ABCD的周长为y. 
(1)求出y关于x的函数f(x)的解析式;
(2)求y的最大值,并指出相应的x值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】不等式2x2﹣x﹣3>0解集为( )
A.{x|﹣1<x< ![]() }??
}??
B.{x|x> ![]() 或x<﹣1}??
或x<﹣1}??
C.{x|﹣ ![]() <x<1}??
<x<1}??
D.{x|x>1或x<﹣ ![]() }
}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式x2﹣ax+b<0的解集为(1,2),则不等式 ![]() <
< ![]() 的解集为( )
的解集为( )
A.( ![]() ,+∞)
,+∞)
B.(﹣∞,0)∪( ![]() ,+∞)
,+∞)
C.( ![]() ,+∞)
,+∞)
D.(﹣∞,0)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() 上的所有点横坐标伸长为原来的
上的所有点横坐标伸长为原来的![]() 倍,纵坐标伸长为原来的2倍后,得到曲线
倍,纵坐标伸长为原来的2倍后,得到曲线![]() ,在以
,在以![]() 为极点,
为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)写出曲线![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离
的距离![]() 最大,并求出此最大值.
最大,并求出此最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com