
已知函数
 为自然对数的底数).
为自然对数的底数).
(1)求曲线 在
在 处的切线方程;
处的切线方程;
(2)若 是
是 的一个极值点,且点
的一个极值点,且点 ,
, 满足条件:
满足条件: .
.
(ⅰ)求 的值;
的值;
(ⅱ)求证:点 ,
, ,
, 是三个不同的点,且构成直角三角形.
是三个不同的点,且构成直角三角形.
(1) ;(2)(ⅰ)
;(2)(ⅰ)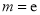 ;(ⅱ)参考解析
;(ⅱ)参考解析
【解析】
试题分析:(1)由函数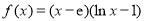 ,求函数
,求函数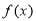 的导数,并计算
的导数,并计算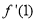 即所求切线方程的斜率,又过点
即所求切线方程的斜率,又过点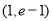 .即可求出结论.
.即可求出结论.
(2)(ⅰ)由(1)得到的函数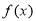 的导数,即可求出函数的单调区间,从而得到函数的极值点,即得到
的导数,即可求出函数的单调区间,从而得到函数的极值点,即得到 的值.
的值.
(ⅱ)需求证:点 ,
,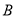 ,
, 是三个不同的点,通过分类每两个点重合,利用已知条件即方程的根的个数来判定即可得到三点是不同点的点.通过向量的数量积可得到三点可构成直角三角形.
是三个不同的点,通过分类每两个点重合,利用已知条件即方程的根的个数来判定即可得到三点是不同点的点.通过向量的数量积可得到三点可构成直角三角形.
(1) , 2分
, 2分
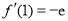 ,又
,又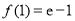 , 4分
, 4分
所以曲线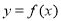 在
在 处的切线方程为
处的切线方程为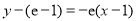 ,
,
即 . 5分
. 5分
(2)(ⅰ)对于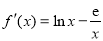 ,定义域为
,定义域为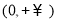 .
.
当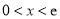 时,
时, ,
, ,∴
,∴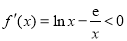 ;
;
当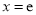 时,
时,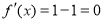 ;
;
当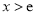 时,
时,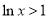 ,
,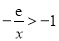 ,∴
,∴ , 8分
, 8分
所以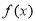 存在唯一的极值点
存在唯一的极值点 ,∴
,∴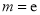 ,则点
,则点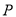 为
为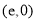 . 9分
. 9分
(ⅱ)若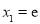 ,则
,则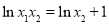 ,
,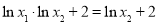 ,
,
与条件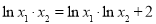 不符,从而得
不符,从而得 .
.
同理可得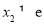 . 10分
. 10分
若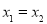 ,由
,由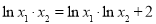
 ,此方程无实数解,
,此方程无实数解,
从而得 . 11分
. 11分
由上可得点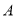 ,
,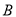 ,
,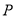 两两不重合.
两两不重合.
又
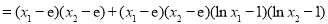

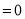
从而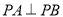 ,点
,点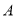 ,
,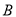 ,
,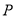 可构成直角三角形. 14分
可构成直角三角形. 14分
考点:1.导数的几何意义.2.函数的极值.3.分类讨论的数学思想.4.向量的数量积.5.运算能力.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源:2013-2014学年福建省漳州市毕业班质量检查理科数学试卷(解析版) 题型:选择题
已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则z=-x+y的取值范围是
A.(1-,2) B.(0,2) C.(-1,2) D.(0,1+)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查理科数学试卷(解析版) 题型:选择题
在二项式 的展开式中恰好第5项的二项式系数最大,则展开式中含
的展开式中恰好第5项的二项式系数最大,则展开式中含 项的系数是( )
项的系数是( )
A.-56 B.-35 C.35 D.56
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查文科数学试卷(解析版) 题型:解答题
某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在
份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在 的学生人数为6.
的学生人数为6.
(1)估计所抽取的数学成绩的众数;
(2)用分层抽样的方法在成绩为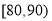 和
和 这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在
这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在 恰有1人的概率.
恰有1人的概率.

查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省三明市高三5月质量检查文科数学试卷(解析版) 题型:选择题
对于函数 在定义域内的任意实数
在定义域内的任意实数 及
及 ,都有
,都有 及
及
 成立,则称函数
成立,则称函数 为“
为“ 函数”.现给出下列四个函数:
函数”.现给出下列四个函数:


 ;
; .其中是“
.其中是“ 函数”的是( )
函数”的是( )
A. B.
B. C.
C.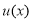 D.
D.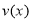
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练四(解析版) 题型:选择题
已知定义在R上的函数f(x),其导函数f′(x)的图象如图所示,则下列叙述正确的是( )

A.f(b)>f(c)>f(d)
B.f(b)>f(a)>f(e)
C.f(c)>f(b)>f(a)
D.f(c)>f(e)>f(d)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年甘肃省武威市高三数学专题训练选择填空限时练二(解析版) 题型:填空题
已知f(x)=aln x+ x2(a>0),若对任意两个不等的正实数x1,x2都有
x2(a>0),若对任意两个不等的正实数x1,x2都有 >2恒成立,则a的取值范围是________.
>2恒成立,则a的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com