
【题目】已知函数![]() ,
,![]() .
.
![]() Ⅰ
Ⅰ![]() 记
记![]() 在
在![]() 上的最大值为M,最小值为m.
上的最大值为M,最小值为m.
![]() 若
若![]() ,求a的取值范围;
,求a的取值范围;
![]() 证明:
证明:![]() ;
;
![]() Ⅱ
Ⅱ![]() 若
若![]() 在
在![]() 上恒成立,求a的最大值.
上恒成立,求a的最大值.
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
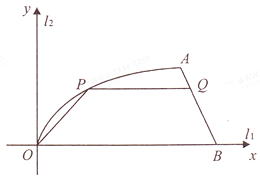
【题目】如图,某小区内有两条互相垂直的道路![]() 与
与![]() ,平面直角坐标系
,平面直角坐标系![]() 的第一象限有一块空地
的第一象限有一块空地![]() ,其边界
,其边界![]() 是函数
是函数![]() 的图象,前一段曲线
的图象,前一段曲线![]() 是函数
是函数![]() 图象的一部分,后一段
图象的一部分,后一段![]() 是一条线段.测得
是一条线段.测得![]() 到
到![]() 的距离为8米,到
的距离为8米,到![]() 的距离为16米,
的距离为16米,![]() 长为20米.
长为20米.
(1)求函数![]() 的解析式;
的解析式;
(2)现要在此地建一个社区活动中心,平面图为梯形![]() (其中
(其中![]() ,
,![]() 为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
为两底边),问:梯形的高为多少米时,该社区活动中心的占地面积最大,并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以A表示值域为R的函数组成的集合,B表示具有如下性质的函数φ(x)组成的集合:对于函数φ(x),存在一个正数M,使得函数φ(x)的值域包含于区间[﹣M,M].例如,当φ1(x)=x3 , φ2(x)=sinx时,φ1(x)∈A,φ2(x)∈B.现有如下命题:
①设函数f(x)的定义域为D,则“f(x)∈A”的充要条件是“b∈R,a∈D,f(a)=b”;
②函数f(x)∈B的充要条件是f(x)有最大值和最小值;
③若函数f(x),g(x)的定义域相同,且f(x)∈A,g(x)∈B,则f(x)+g(x)B.
④若函数f(x)=aln(x+2)+ ![]() (x>﹣2,a∈R)有最大值,则f(x)∈B.
(x>﹣2,a∈R)有最大值,则f(x)∈B.
其中的真命题有 . (写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高一年级共有20个班,为参加全市的钢琴比赛,调查了各班中会弹钢琴的人数,并以组距为5将数据分组成![]() 时,作出如下频率分布直方图.
时,作出如下频率分布直方图.
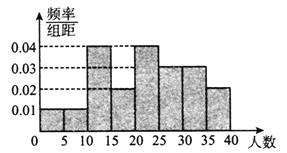
(Ⅰ)由频率分布直方图估计各班中会弹钢琴的人数的平均值;
(Ⅱ)若会弹钢琴的人数为![]() 的班级作为第一备选班级,会弹钢琴的人数为
的班级作为第一备选班级,会弹钢琴的人数为![]() 的班级作为第二备选班级,现要从这两类备选班级中选出两个班参加市里的钢琴比赛,求这两类备选班级中均有班级被选中的概率.
的班级作为第二备选班级,现要从这两类备选班级中选出两个班参加市里的钢琴比赛,求这两类备选班级中均有班级被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
=1(a>b>0)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线x=﹣3上任意一点,过F作TF的垂线交椭圆C于点P,Q.
①证明:OT平分线段PQ(其中O为坐标原点);
②当 ![]() 最小时,求点T的坐标.
最小时,求点T的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于直线l:ax+by+c=0和点P1(x1 , y1),P2(x2 , y2),记η=(ax1+by1+c)(ax2+by2+c),若η<0,则称点P1 , P2被直线l分隔,若曲线C与直线l没有公共点,且曲线C上存在点P1、P2被直线l分隔,则称直线l为曲线C的一条分隔线.
(1)求证:点A(1,2),B(﹣1,0)被直线x+y﹣1=0分隔;
(2)若直线y=kx是曲线x2﹣4y2=1的分隔线,求实数k的取值范围;
(3)动点M到点Q(0,2)的距离与到y轴的距离之积为1,设点M的轨迹为曲线E,求证:通过原点的直线中,有且仅有一条直线是E的分隔线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】狄利克雷函数是高等数学中的一个典型函数,若![]() ,则称
,则称![]() 为狄利克雷函数.对于狄利克雷函数
为狄利克雷函数.对于狄利克雷函数![]() ,给出下面4个命题:①对任意
,给出下面4个命题:①对任意![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ;③对任意
;③对任意![]() ,都有
,都有![]() ,
, ![]() ;④对任意
;④对任意![]() ,都有
,都有![]() .其中所有真命题的序号是( )
.其中所有真命题的序号是( )
A. ①④ B. ②③ C. ①②③ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的奇函数且f(-2)=-3,当x≥0时,f(x)=ax-1,其中a>0且a≠1.
(1)求![]() 的值;
的值;
(2)求函数f(x)的解析式;
(3)已知g(x)=log2x,若对任意的x1∈[1,4],存在![]() 使得f(mx1)+1≥g(x2)(其中m≥0)成立,求实数m的取值范围.
使得f(mx1)+1≥g(x2)(其中m≥0)成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com