
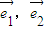 不平行,那么
不平行,那么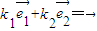 (k1,k2∈R)的充要条件是k1=k2=0”.试用上述定理解答问题:
(k1,k2∈R)的充要条件是k1=k2=0”.试用上述定理解答问题: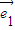 与
与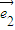 不平行.已知向量
不平行.已知向量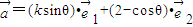 ,向量
,向量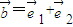 ,且
,且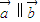 .求k与θ的关系式;并当θ∈R时,求k的取值范围.
.求k与θ的关系式;并当θ∈R时,求k的取值范围. ,可根据向量平行的充要条件,找到
,可根据向量平行的充要条件,找到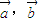 坐标之间的关系,再根据题目中给出的定理,化简,即可得到k与θ的关系式,把关系式看作过定点与动点的直线的斜率,利用直线与圆相切的判断,求出k的范围即可.
坐标之间的关系,再根据题目中给出的定理,化简,即可得到k与θ的关系式,把关系式看作过定点与动点的直线的斜率,利用直线与圆相切的判断,求出k的范围即可.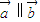 ,∴存在唯一实数λ,使
,∴存在唯一实数λ,使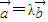 ,即
,即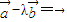
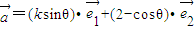 ,
,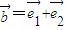 ,
,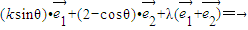
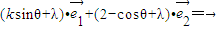
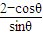
 可看作点(-sinθ,cosθ),与点(0,2)连线的斜率
可看作点(-sinθ,cosθ),与点(0,2)连线的斜率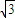
 <k<
<k<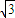
 ,当θ∈R时,k的取值范围为(-
,当θ∈R时,k的取值范围为(-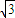 ,
,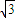 )
)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| e1 |
| e2 |
| e1 |
| e2 |
| 0 |
| e1 |
| e2 |
| a |
| e |
| e |
| b |
| e |
| e |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源: 题型:022
正弦定理在解三角形中的作用:
(1)
如果已知三角形的任意两个______与一_______,由三角形________,可以计算出三角形的另一________,并由正弦定理计算出三角形的另_______.(2)
如果已知三角形的任意________与基中一边的______,应用正弦定理,可以计算出另一边的对角的_______,进而确定这个_______和三角形其他的_______.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
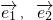 不平行,那么
不平行,那么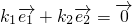 (k1,k2∈R)的充要条件是k1=k2=0”.试用上述定理解答问题:
(k1,k2∈R)的充要条件是k1=k2=0”.试用上述定理解答问题: 与
与 不平行.已知向量
不平行.已知向量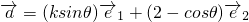 ,向量
,向量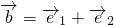 ,且
,且 .求k与θ的关系式;并当θ∈R时,求k的取值范围.
.求k与θ的关系式;并当θ∈R时,求k的取值范围.查看答案和解析>>
科目:高中数学 来源:普陀区二模 题型:解答题
| e1 |
| e2 |
| e1 |
| e2 |
| 0 |
| e1 |
| e2 |
| a |
| e |
| e |
| b |
| e |
| e |
| a |
| b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com