
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: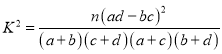 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)
某单位建造一间地面面积为12m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过![]() 米,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.
米,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m,且不计房屋背面的费用.
(1)把房屋总造价![]() 表示成
表示成![]() 的函数,并写出该函数的定义域.
的函数,并写出该函数的定义域.
(2)当侧面的长度为多少时,总造价最底?最低总造价是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且Sn=n(n+2)(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场在促销期间规定:商场内所有商品按标价的![]() 出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
出售,当顾客在商场内消费一定金额后,按如下方案获得相应金额的奖券:
消费金额(元)的范围 |
|
|
|
| … |
获得奖券的金额(元) | 30 | 60 | 100 | 130 | … |
根据上述促销方法,顾客在该商场购物可以获得双重优惠,例如:购买标价为400元的商品,则消费金额为320元,获得的优惠额为:![]() 元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
元,设购买商品得到的优惠率=(购买商品获得的优惠额)/(商品标价),试问:
(1)若购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)对于标价在![]() (元)内的商品,顾客购买标价为多少元的商品,可得到不小于
(元)内的商品,顾客购买标价为多少元的商品,可得到不小于![]() 的优惠率?
的优惠率?
查看答案和解析>>
科目:高中数学 来源: 题型:
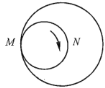
【题目】如图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方向滚动,M和N是小圆的一条固定直径的两个端点,那么,当小圆这样滚过大圆内壁的一周,点M,N在大圆内所绘出的图形大致是( )
A. B.
B. C.
C.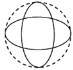 D.
D.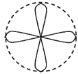
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为
为![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交
交![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 的横坐标为
的横坐标为![]() 时,
时,![]() 为正三角形.
为正三角形.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)若直线![]() ,且
,且![]() 和
和![]() 有且只有一个公共点
有且只有一个公共点![]() ,
,
(ⅰ)证明直线![]() 过定点,并求出定点坐标;
过定点,并求出定点坐标;
(ⅱ)![]() 的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 为椭圆
为椭圆![]() :
:![]() 的右焦点,过
的右焦点,过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 、
、![]() 斜率的乘积为
斜率的乘积为![]() ,两直线
,两直线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() 、
、![]() 、
、![]() 、
、![]() 四点,求四边形
四点,求四边形![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com