
【题目】在平面直角坐标系![]() 中,点
中,点![]() 为椭圆
为椭圆![]() :
:![]() 的右焦点,过
的右焦点,过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 、
、![]() 斜率的乘积为
斜率的乘积为![]() ,两直线
,两直线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() 、
、![]() 、
、![]() 、
、![]() 四点,求四边形
四点,求四边形![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设![]() ,
,![]() ,
,![]() ,
,![]() ,利用点差法求出直线
,利用点差法求出直线![]() 的斜率为:
的斜率为:![]() ,又直线
,又直线![]() 的斜率为:
的斜率为: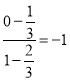 ,所以
,所以![]() ,得到
,得到![]() ,再结合
,再结合![]() ,
,![]() ,即可求出
,即可求出![]() ,
,![]() ,
,![]() 的值,从而求得椭圆
的值,从而求得椭圆![]() 的方程;
的方程;
(2)设点![]() ,
,![]() ,
,![]() ,
,![]() ,由题意可知
,由题意可知![]() ,当直线
,当直线![]() 的斜率不存在时,易求四边形
的斜率不存在时,易求四边形![]() 的面积
的面积![]() ,当直线
,当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为:
的方程为:![]() ,与椭圆方程联立,利用韦达定理代入
,与椭圆方程联立,利用韦达定理代入![]() 得
得![]() ,再由弦长公式和点到直线距离公式求得
,再由弦长公式和点到直线距离公式求得![]() ,由椭圆的对称性可知:四边形
,由椭圆的对称性可知:四边形![]() 的面积为
的面积为![]() ,从而得到边形
,从而得到边形![]() 的面积为
的面积为![]() .
.
(1)由题意可知,![]() ,设
,设![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
又∵点![]() ,
,![]() 在椭圆上,∴
在椭圆上,∴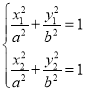 ,两式相减得:
,两式相减得:![]() ,
,
∴![]() ,即直线
,即直线![]() 的斜率为:
的斜率为:![]() ,
,
又∵直线![]() 过右焦点
过右焦点![]() ,过点
,过点![]() ,∴直线
,∴直线![]() 的斜率为:
的斜率为: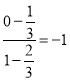 ,
,
∴![]() ,∴
,∴![]() ,又∵
,又∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,∴椭圆
,∴椭圆![]() 的方程为:
的方程为:![]() ;
;
(2)设点![]() ,
,![]() ,
,
由题意可知,![]() ,即
,即![]() ,①当直线
,①当直线![]() 的斜率不存在时,显然
的斜率不存在时,显然![]() ,
,![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]() ,
,![]() ,
,
∴四边形![]() 的面积
的面积![]() ,
,
②当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为:
的方程为:![]() ,
,
联立方程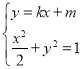 ,消去
,消去![]() 得:
得:![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
整理得:![]() ,
,
由弦长公式得: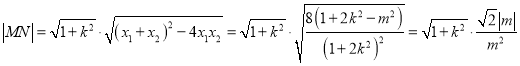 ,
,
原点(0,0)到直线![]() 的距离
的距离![]() ,
,
∴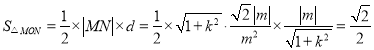 ,
,
由椭圆的对称性可知:四边形![]() 的面积为
的面积为![]() ,
,
综上所述,四边形![]() 的面积为
的面积为![]() .
.


科目:高中数学 来源: 题型:
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: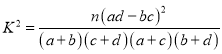 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了防止受到核污染的产品影响我国民众的身体健康,要求产品在进入市场前必须进行两轮核辐射检测,只有两轮都合格才能进行销售,否则不能销售.已知某产品第一轮检测不合格的概率为![]() ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为![]() ,两轮检测是否合格相互没有影响.若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则P(X≥-80)=________.
,两轮检测是否合格相互没有影响.若产品可以销售,则每件产品获利40元;若产品不能销售,则每件产品亏损80元.已知一箱中有4件产品,记一箱产品获利X元,则P(X≥-80)=________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】统计与人类活动息息相关,我国从古代就形成了一套关于统计和整理数据的方法.据宋元时代学者马端临所著的《文献通考》记载,宋神宗熙宁年间(公元1068-1077年),天下诸州商税岁额:四十万贯以上者三,二十万贯以上者五,十万贯以上者十九……五千贯以下者七十三,共计三百十一.由这段内容我们可以得到如下的统计表格:
分组(万贯) |
|
|
|
|
|
|
|
| 合计 |
合计 | 73 | 35 | 95 | 51 | 30 | 19 | 5 | 3 | 311 |
则宋神宗熙宁年间各州商税岁额(单位:万贯)的中位数大约为( )
A.0.5B.2C.5D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 为椭圆
为椭圆![]() :
:![]() 的右焦点,过
的右焦点,过![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 、
、![]() 斜率的乘积为
斜率的乘积为![]() ,两直线
,两直线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() 、
、![]() 、
、![]() 、
、![]() 四点,求四边形
四点,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
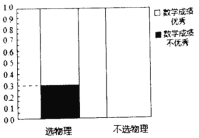
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附: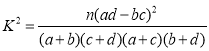
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,以下关于
,以下关于![]() 的结论其中正确的结论是( )
的结论其中正确的结论是( )
①当![]() 时,
时,![]() 在
在![]() 上无零点;
上无零点;
②当![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
③当![]() 时,
时,![]() 在
在![]() 上有无数个极值点;
上有无数个极值点;
④当![]() 时,
时,![]() 在
在![]() 上恒成立.
上恒成立.
A.①④B.②③C.①②④D.②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆规是用来画椭圆的一种器械,它的构造如图所示,在一个十字形的金属板上有两条互相垂直的导槽,在直尺上有两个固定的滑块A,B,它们可分别在纵槽和横槽中滑动,在直尺上的点M处用套管装上铅笔,使直尺转动一周,则点M的轨迹C是一个椭圆,其中|MA|=2,|MB|=1,如图,以两条导槽的交点为原点O,横槽所在直线为x轴,建立直角坐标系.
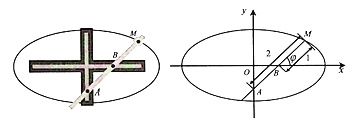
(1)将以射线Bx为始边,射线BM为终边的角xBM记为φ(0≤φ<2π),用![]() 表示点M的坐标,并求出C的普通方程;
表示点M的坐标,并求出C的普通方程;
(2)已知过C的左焦点F,且倾斜角为α(0≤α![]() )的直线l1与C交于D,E两点,过点F且垂直于l1的直线l2与C交于G,H两点.当
)的直线l1与C交于D,E两点,过点F且垂直于l1的直线l2与C交于G,H两点.当![]() ,|GH|,
,|GH|,![]() 依次成等差数列时,求直线l2的普通方程.
依次成等差数列时,求直线l2的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l过定点P(0,1),且与直线l1:x-3y+10=0,l2:2x+y-8=0分别交于A、B两点.若线段AB的中点为P,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com