
【题目】椭圆规是用来画椭圆的一种器械,它的构造如图所示,在一个十字形的金属板上有两条互相垂直的导槽,在直尺上有两个固定的滑块A,B,它们可分别在纵槽和横槽中滑动,在直尺上的点M处用套管装上铅笔,使直尺转动一周,则点M的轨迹C是一个椭圆,其中|MA|=2,|MB|=1,如图,以两条导槽的交点为原点O,横槽所在直线为x轴,建立直角坐标系.
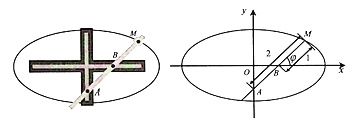
(1)将以射线Bx为始边,射线BM为终边的角xBM记为φ(0≤φ<2π),用![]() 表示点M的坐标,并求出C的普通方程;
表示点M的坐标,并求出C的普通方程;
(2)已知过C的左焦点F,且倾斜角为α(0≤α![]() )的直线l1与C交于D,E两点,过点F且垂直于l1的直线l2与C交于G,H两点.当
)的直线l1与C交于D,E两点,过点F且垂直于l1的直线l2与C交于G,H两点.当![]() ,|GH|,
,|GH|,![]() 依次成等差数列时,求直线l2的普通方程.
依次成等差数列时,求直线l2的普通方程.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)用三角函数表示出点M的坐标,直接利用转换关系把极坐标方程转换为直角坐标方程;(2)设出直线l1的参数方程,与椭圆方程联立利用直线参数的几何意义求出![]() 、
、![]() ,根据题意有
,根据题意有![]() ,列出方程求出直线l1的斜率即可求得直线l2的方程.
,列出方程求出直线l1的斜率即可求得直线l2的方程.
(1)设M(x,y)依题意得:x=2cosφ,y=sinφ,
所以M(2cosφ,sinφ),
由于cos2φ+sin2φ=1,整理得![]() .
.
(2)由于直线l1的倾斜角为α(![]() ),且l1⊥l2,
),且l1⊥l2,
所以直线l2的倾斜角为![]() ,依题意易知:F(
,依题意易知:F(![]() ),
),
可设直线l1的方程为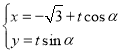 (t为参数),
(t为参数),
代入![]() 得到:
得到:![]() ,
,
易知![]() ,
,
设点D和点E对应的参数为t1和t2,
所以![]() ,
,![]() .
.
则![]() ,
,
由参数的几何意义: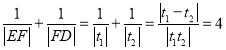 ,
,
设G、H对应的参数为t3和t4,同理对于直线l2,将α换为![]() ,
,
所以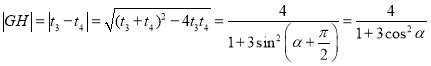 ,
,
由于![]() ,|GH|,
,|GH|,![]() 依次成等差数列,
依次成等差数列,
所以![]() ,则
,则![]() ,解得
,解得![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() ,
,
所以直线l2的斜率为![]() ,直线l2的直角坐标方程为x
,直线l2的直角坐标方程为x![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“团购”已经渗透到我们每个人的生活,这离不开快递行业的发展,下表是2013-2017年全国快递业务量(x亿件:精确到0.1)及其增长速度(y%)的数据
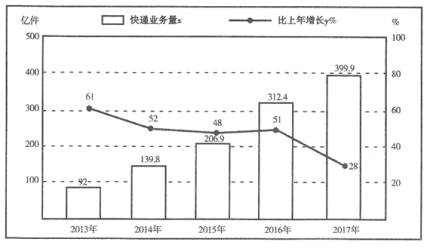
(1)试计算2012年的快递业务量;
(2)分别将2013年,2014年,…,2017年记成年的序号t:1,2,3,4,5;现已知y与t具有线性相关关系,试建立y关于t的回归直线方程![]() ;
;
(3)根据(2)问中所建立的回归直线方程,估算2019年的快递业务量
附:回归直线的斜率和截距地最小二乘法估计公式分别为: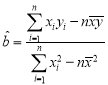 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着现代电子技术的迅猛发展,关于元件和系统可靠性的研究已发展成为一门新的学科——可靠性理论.在可靠性理论中,一个元件正常工作的概率称为该元件的可靠性.元件组成系统,系统正常工作的概率称为该系统的可靠性.现有![]() (
(![]() ,
,![]() )种电子元件,每种2个,每个元件的可靠性均为
)种电子元件,每种2个,每个元件的可靠性均为![]() (
(![]() ).当某元件不能正常工作时,该元件在电路中将形成断路.现要用这
).当某元件不能正常工作时,该元件在电路中将形成断路.现要用这![]() 个元件组成一个电路系统,有如下两种连接方案可供选择,当且仅当从A到B的电路为通路状态时,系统正常工作.
个元件组成一个电路系统,有如下两种连接方案可供选择,当且仅当从A到B的电路为通路状态时,系统正常工作.
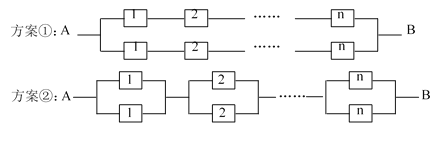
(1)(i)分别写出按方案①和方案②建立的电路系统的可靠性![]() 、
、![]() (用
(用![]() 和
和![]() 表示);
表示);
(ii)比较![]() 与
与![]() 的大小,说明哪种连接方案更稳定可靠;
的大小,说明哪种连接方案更稳定可靠;
(2)设![]() ,
,![]() ,已知按方案②建立的电路系统可以正常工作,记此时系统中损坏的元件个数为
,已知按方案②建立的电路系统可以正常工作,记此时系统中损坏的元件个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与函数
与函数![]() (
(![]() )的图象相交,将其中三个相邻交点从左到右依次记为A,B,C,且满足
)的图象相交,将其中三个相邻交点从左到右依次记为A,B,C,且满足![]()
![]() 有下列结论:
有下列结论:
①n的值可能为2
②当![]() ,且
,且![]() 时,
时,![]() 的图象可能关于直线
的图象可能关于直线![]() 对称
对称
③当![]() 时,有且仅有一个实数ω,使得
时,有且仅有一个实数ω,使得![]() 在
在![]() 上单调递增;
上单调递增;
④不等式![]() 恒成立
恒成立
其中所有正确结论的编号为( )
A.③B.①②C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥![]() 中,底面
中,底面![]() 是边长为4的正方形,
是边长为4的正方形,![]() 为正三角形,
为正三角形,![]() 是
是![]() 的中点,过
的中点,过![]() 的平面
的平面![]() 平行于平面
平行于平面![]() ,且平面
,且平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,与平面
,与平面![]() 的交线为
的交线为![]() .
.
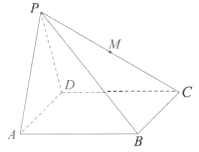
(1)在图中作出四边形![]() (不必说出作法和理由);
(不必说出作法和理由);
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 形成的锐二面角的余弦值.
形成的锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.
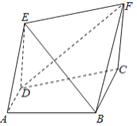
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,政府相关部门引导乡村发展旅游的同时,鼓励农户建设温室大棚种植高品质农作物.为了解某农作物的大棚种植面积对种植管理成本的影响,甲,乙两同学一起收集6家农户的数据,进行回归分折,得到两个回归摸型:模型①:![]() ,模型②:
,模型②: ![]() ,对以上两个回归方程进行残差分析,得到下表:
,对以上两个回归方程进行残差分析,得到下表:
种植面积 | 2 | 3 | 4 | 5 | 7 | 9 | |
每亩种植管理成本 | 25 | 24 | 21 | 22 | 16 | 14 | |
模型① | 估计值 | 25.27 | 23.62 | 21.97 | 17.02 | 13.72 | |
残差 | -0.27 | 0.38 | -0.97 | -1.02 | 0.28 | ||
模型② |
| 26.84 | 20.17 | 18.83 | 17.31 | 16.46 | |
| -1.84 | 0.83 | 3.17 | -1.31 | -2.46 | ||
(1)将以上表格补充完整,并根据残差平方和判断哪个模型拟合效果更好;
(2)视残差![]() 的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
的绝对值超过1.5的数据视为异常数据,针对(1)中拟合效果较好的模型,剔除异常数据后,重新求回归方程.
附: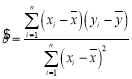 ,
,![]() ;
;![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com