
分析 由题意可知2an+1+Sn=3(n∈N*),2an+2+Sn+1=3,2an+2+Sn+1-2an+1-Sn=0,求得2an+2=an+1,数列{an}是公比q=$\frac{1}{2}$,首项a1=2的等比数列,则Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$=4-4($\frac{1}{2}$)n,$\frac{{{S_{2n}}}}{S_n}$=$\frac{4-4•(\frac{1}{2})^{2n}}{4-4•(\frac{1}{2})^{n}}$=1+($\frac{1}{2}$)n,则$\frac{34}{33}$<1+($\frac{1}{2}$)n<$\frac{16}{15}$,即可求得n的所有值,求得满足$\frac{34}{33}$<$\frac{{{S_{2n}}}}{S_n}$<$\frac{16}{15}$的所有n的和.
解答 解:由2an+1+Sn=3(n∈N*),
∴2an+2+Sn+1=3,
两式相减得2an+2+Sn+1-2an+1-Sn=0,
即2an+2+an+1-2an+1=0,
则2an+2=an+1,
当n=1时,2a2+a1=3,
则a2=$\frac{1}{2}$,满足2a2=a1,
即2an+1=an,则$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{1}{2}$,即数列{an}是公比q=$\frac{1}{2}$,首项a1=2的等比数列,
则数列{an}前n项和为Sn=$\frac{{a}_{1}(1-{q}^{n})}{1-q}$=4-4($\frac{1}{2}$)n,
∴$\frac{{{S_{2n}}}}{S_n}$=$\frac{4-4•(\frac{1}{2})^{2n}}{4-4•(\frac{1}{2})^{n}}$=1+($\frac{1}{2}$)n,
∵$\frac{34}{33}$<$\frac{{{S_{2n}}}}{S_n}$<$\frac{16}{15}$,即$\frac{34}{33}$<1+($\frac{1}{2}$)n<$\frac{16}{15}$,
$\frac{1}{33}$<($\frac{1}{2}$)n<$\frac{1}{15}$,
则15<2n<33,
则n=4或5,
则4+5=9,
故答案为:9.
点评 本题主要考查递推数列的应用,根据递推数列得到数列通项公式及前n项和公式的应用,指数函数比较大小,考查计算能力,属于中档题.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
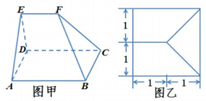 多面体ABCDEF(如图甲)的俯视图如图乙,己知面ADE为正三角形.
多面体ABCDEF(如图甲)的俯视图如图乙,己知面ADE为正三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com