
(1)求证:an=n-1;
(2)求bn的表达式;
(3)cn=-an·bn,试问数列{cn}中,是否存在正整数k,使得对于任意的正整数n,都有cn≤ck成立?证明你的结论.
(1)证明:y=a·b=x2+(n+4)x-3,因为对称轴x=![]() ,所以在[0,1]上为增函数.
,所以在[0,1]上为增函数.
所以an=(-3)+(n+2)=n-1.
(2)解:由nb1+(n-1)b2+…+2bn-1+bn=(![]() )n-1+(
)n-1+(![]() )n-2+…+
)n-2+…+![]() +1,
+1,
得(n-1)b1+(n-2)b2+…+bn-1=(![]() )n-2+(
)n-2+(![]() )n-3+…+
)n-3+…+![]() +1,
+1,
两式相减,得b1+b2+…+bn-1+bn=(![]() )n-1=Sn,
)n-1=Sn,
当n=1时,b1=S1=1;
当n≥2时,bn=Sn-Sn-1=![]() (
(![]() )n-2,
)n-2,
即bn=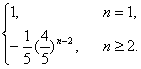
(3)解:由(1)与(2)得
cn=-an·bn=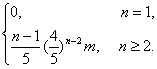
设存在正整数k,使得对于任意的正整数n,都有cn≤ck成立,
当n=1时,c2-c1=![]() >0
>0![]() c2>c1.
c2>c1.
当n≥2时,cn+1-cn=(![]() )n-2·
)n-2·![]() ,
,
所以当n<5时,cn+1>cn;
当n=5时,cn+1=cn;
当n>5时,cn+1<cn.
所以存在正整数k=5,使得对于任意的正整数n,都有cn≤ck成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| 9 |
| 10 |
| 9 |
| 10 |
| 9 |
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.(-![]() ,-5)B.(-1,-2)C.(
,-5)B.(-1,-2)C.(![]() ,5)D.(1,2)
,5)D.(1,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com