
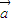 =(cosx+sinx,sinx).
=(cosx+sinx,sinx). =(cosx-sinx,2cosx),设f(x)=
=(cosx-sinx,2cosx),设f(x)=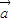 •
• .
. ,f(B)=1,
,f(B)=1,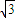 a+
a+ b=10,求边c.
b=10,求边c.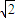 sin(2x+
sin(2x+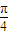 ),由-
),由- +2kπ≤2x+
+2kπ≤2x+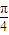 ≤
≤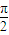 +2kπ即可求得函数f(x)的单调增区间;
+2kπ即可求得函数f(x)的单调增区间; ,由正弦定理可设设
,由正弦定理可设设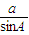 =
=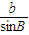 =
=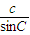 =k,结合题意可得k=4,从而可求得c.
=k,结合题意可得k=4,从而可求得c.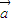 •
•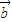 =cos2x+sin2x=
=cos2x+sin2x=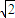 sin(2x+
sin(2x+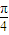 ),…(3分)
),…(3分)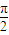 +2kπ≤2x+
+2kπ≤2x+ ≤
≤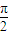 +2kπ得由f(x)递增得:-
+2kπ得由f(x)递增得:-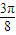 +kπ≤x≤
+kπ≤x≤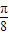 +kπ,k∈Z,
+kπ,k∈Z,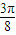 +kπ,
+kπ,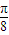 +kπ],k∈Z. …(6分)
+kπ],k∈Z. …(6分)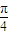 )=
)=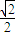 及0<B<π得B=
及0<B<π得B=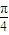 ,…(8分)
,…(8分)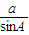 =
= =
= =k,则
=k,则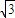 ksin
ksin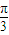 +
+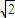 ksin
ksin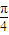 =10,
=10, k=10,k=4 …(10分)
k=10,k=4 …(10分)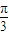 cos
cos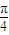 +cos
+cos sin
sin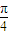 )=
)=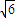 +
+ .…(12分)
.…(12分)

科目:高中数学 来源: 题型:
| 3 |
| π |
| 2 |
| 6 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| 3 |
| n |
| m |
| n |
| π |
| 2 |
| 6 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012年浙江省高考数学冲刺试卷3(理科)(解析版) 题型:解答题
 =(
=( cosx+
cosx+ sinx,cosx),
sinx,cosx), =(cosx-sinx,2sinx),f(x)=
=(cosx-sinx,2sinx),f(x)= •
• .
. ,b=2c,a=2
,b=2c,a=2 ,求S△ABC.
,求S△ABC.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| m |
| 3 |
| n |
| m |
| n |
| π |
| 2 |
| 6 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:浙江省模拟题 题型:解答题
 cosx+
cosx+ sinx,cosx),β=(cosx-sinx,2sinx),f(x)= α·β。
sinx,cosx),β=(cosx-sinx,2sinx),f(x)= α·β。 ,b=2c,a=2
,b=2c,a=2 ,求S△ABC。
,求S△ABC。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com