
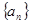 中,
中,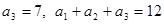 ,令
,令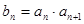 ,数列
,数列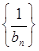 的前
的前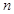 项和为
项和为 .
.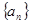 的通项公式;
的通项公式; ;
;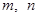 ,且
,且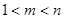 ,使得
,使得 ,
, ,
, 成等比数列?若存在,求出
成等比数列?若存在,求出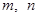 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.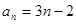 .(2)
.(2)
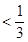 .
.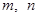 ,且
,且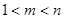 ,使得
,使得 ,
, ,
, 成等比数列.
成等比数列.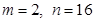 ,且
,且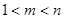 ,使得
,使得 ,
, ,
, 成等比数列.(16分)
成等比数列.(16分)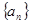 为等差数列,并且
为等差数列,并且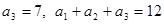 ,易求出
,易求出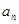 的通项公式,(2)在(1)的基础上可得
的通项公式,(2)在(1)的基础上可得 ,则
,则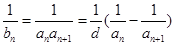 ,再采用裂项求和的方示求和.
,再采用裂项求和的方示求和. ,
, ,
, 成等比数列,则
成等比数列,则 ,即
,即 ,因为
,因为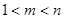 ,所以下面讨论按m=2,3,4,5,6,和
,所以下面讨论按m=2,3,4,5,6,和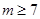 几种情况进行讨论求解.
几种情况进行讨论求解.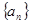 的公差为
的公差为 ,由
,由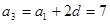 ,
, .
. ,
, ,∴
,∴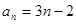 .(4分)
.(4分)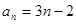 ,
, ,∴
,∴


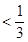 .(8分)
.(8分) ,∴
,∴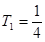 ,
, ,
, ,
,
 ,
, ,
, 成等比数列,∴
成等比数列,∴ ,即
,即
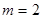 时,
时, ,
, ,符合题意;
,符合题意;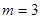 时,
时,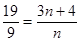 ,
,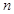 无正整数解;
无正整数解;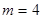 时,
时, ,
,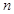 无正整数解;
无正整数解; 时,
时, ,
,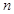 无正整数解;
无正整数解;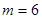 时,
时,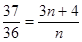 ,
,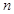 无正整数解;
无正整数解;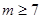 时,
时, ,则
,则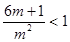 ,而
,而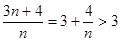 ,
,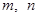 ,且
,且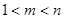 ,使得
,使得 ,
, ,
, 成等比数列.
成等比数列.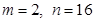 ,且
,且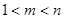 ,使得
,使得 ,
, ,
, 成等比数列.(16分)
成等比数列.(16分)

科目:高中数学 来源:不详 题型:单选题
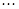 ,则第60个数对是( )
,则第60个数对是( )| A.(3,8) | B.(4,7) | C.(4,8) | D.(5,7) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
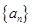 中,
中,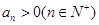 ,公比
,公比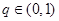 ,且
,且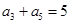 ,又
,又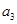 与
与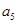 的等比中项为2.
的等比中项为2.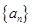 的通项公式;
的通项公式;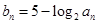 ,数列
,数列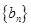 的前
的前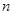 项和为
项和为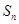 ,求数列
,求数列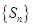 的通项公式;
的通项公式;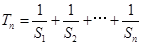 ,求
,求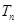 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com