
| 用电量(千瓦时) | [0,100] | (100,200] | (200,300] | (300,400] | (400,500] | 合计 |
| 频数 | 200 | 400 | 200 | b | 100 | 1000 |
| 频率 | 0.2 | a | 0.2 | 0.1 | c | 1 |
分析 (Ⅰ)利用调查的1000户居民,求出b,利用频数与总数的比值直接求解a,c的值;
(Ⅱ)从该市调查的1000户居民中随机抽取一户居民,用电量不超过300千瓦时的有200+400+200=800户,然后求解该户居民用电量不超过300千瓦时的概率;
(Ⅲ)同组中的每个数据用该组区间的中点值代替,然后求解该市每户居民该月的平均电费.
解答 (本小题满分13分)
解:(Ⅰ)a=0.4,b=100,c=0.1.…(3分)
(Ⅱ)设“该户居民月用电量不超过300千瓦时”为事件A.…(4分)
由表可知:共调查了1000户居民,用电量不超过300千瓦时的有200+400+200=800户,用电量超过300千瓦时的有100+100=200户,
所以该居民月用电量不超过300千瓦时的概率$P(A)=\frac{800}{1000}=\frac{4}{5}$.…(8分)
(Ⅲ)由用电量的频率分布表和题意,得居民该月用电费用的数据分组与频率分布表:
| 用电量(千瓦时) | [0,100] | (100,200] | (200,300] | (300,400] | (400,500] |
| 用电费用 | [0,50] | (50,100] | (100,160] | (160,220] | (220,300] |
| 频率 | 0.2 | 0.4 | 0.2 | 0.1 | 0.1 |
点评 本题考查频率分布直方图的应用,概率的求法,考查计算能力,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 数学分数x | 89 | 91 | 93 | 95 | 97 |
| 物理分数y | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
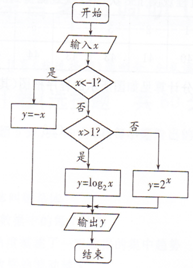 某算法的程序框图如图所示.如果从集合{x|-5≤x≤5,x∈Z}中任取一个数作为x值输入,则输出的y值大于或等于3的概率为( )
某算法的程序框图如图所示.如果从集合{x|-5≤x≤5,x∈Z}中任取一个数作为x值输入,则输出的y值大于或等于3的概率为( )| A. | $\frac{3}{10}$ | B. | $\frac{3}{11}$ | C. | $\frac{7}{10}$ | D. | $\frac{7}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com