
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 数学分数x | 89 | 91 | 93 | 95 | 97 |
| 物理分数y | 87 | 89 | 89 | 92 | 93 |
分析 (1)按性别比例分层抽样,可以得到${C}_{36}^{3}{C}_{24}^{2}$个不同的样本;
(2)①根据题目中的公式,计算相关系数r,判断线性相关性;②求出线性回归方程中的系数,得出回归方程.
解答 解:(1)按性别比例分层抽样,可以得到${C}_{36}^{3}{C}_{24}^{2}$个不同的样本;
(2)①这5位同学中恰有2位同学的数学和物理分数均为优秀,有3人,其概率为$\frac{3}{5}$;
②r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}}$=0.96,有较强的线性相关关系,
$\stackrel{∧}{b}$≈0.75,$\stackrel{∧}{a}$=20.25,线性回归方程是$\stackrel{∧}{y}$=0.75x+20.25.
点评 本题考查了线性回归方程的应用问题,也考查了线性相关系数的计算问题,是基础题目.


科目:高中数学 来源: 题型:选择题
| A. | 2520 | B. | 1440 | C. | -1440 | D. | -2520 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | -9 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
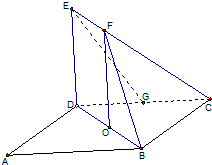 如图,菱形ABCD的中心为O,四边形ODEF为矩形,平面ODEF⊥平面ABCD,DE=DA=DB=2.
如图,菱形ABCD的中心为O,四边形ODEF为矩形,平面ODEF⊥平面ABCD,DE=DA=DB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 用电量(千瓦时) | [0,100] | (100,200] | (200,300] | (300,400] | (400,500] | 合计 |
| 频数 | 200 | 400 | 200 | b | 100 | 1000 |
| 频率 | 0.2 | a | 0.2 | 0.1 | c | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
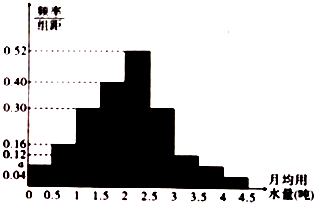
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com