练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．（x+$\frac{a}{x}$）（3x-$\frac{2}{x}$）5的展开式中各项系数的和为3，则该展开式中常数项为（　　）
    A．2520B．1440C．-1440D．-2520

    分析 根据展开式中各项系数的和2求得a的值，再把二项式展开，求得该展开式中常数项．

    解答 解：令x=1可得（x+$\frac{a}{x}$）（3x-$\frac{2}{x}$）5的展开式中各项系数的和为（a+1）=3，∴a=2．
    ∴（x+$\frac{a}{x}$）（3x-$\frac{2}{x}$）5 =（x+$\frac{2}{x}$）（3x-$\frac{2}{x}$）5
    =（x+$\frac{2}{x}$）（ ${C}_{5}^{0}$•243x5-${C}_{5}^{1}$•162x3+${C}_{5}^{2}$•108x-${C}_{5}^{3}$•$\frac{72}{x}$+${C}_{5}^{4}$•$\frac{48}{{x}^{3}}$-${C}_{5}^{5}$•$\frac{32}{{x}^{5}}$），
    故该展开式中常数项为-${C}_{5}^{3}$•72+2•108${C}_{5}^{2}$=1440，
    故选：B．

    点评 本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，求二项展开式各项的系数和的方法，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    13．已知集合M={0，1，2，3}，N={x|x2-x-2≤0}，P=M∩N，则集合P的子集共有（　　）
    A．2个B．4个C．6个D．8个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．设复数z=（m2-2m-15）+（m2+4m+3）i，试求实数m的值，使：
    （1）z是实数；      
    （2）z是纯虚数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

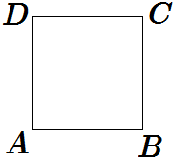    11．质点P从如图放置的正方形ABCD的顶点A出发，根据掷骰子的情况，按照以下的规则在顶点间来回移动：如果朝上数字大于等于5，向平行于AB边的方向移动；如果朝上数字小于等于4，向平行于AD边的方向移动．记掷骰子2n（n∈N*）次后质点P回到A点的概率为an，回到C点的概率为cn．
    （I）求a1的值；
    （II）当n=2时，设X表示质点P到达C点的次数，X的分布列和期望；
    （III）当m=2015时，试比较a2015c2015，$\frac{1}{2}$的大小（只需写出结论）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知不等式x2+px+1＞2x+p，当|p|≤2时恒成立，则实数x的取值范围是（-∞，-1）∪（3，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=$\frac{1+2lnx}{x^2}$．
    （1）求f（x）的单调区间；
    （2）存在x1，x2∈（1，+∞）且x1≠x2，使|f（x1）-f（x2）|≥k|lnx1-lnx2|成立，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知等差数列{an}中，a1=1，a5=-3；
    （1）求数列{an}的通项公式；
    （2）若数列{an}的前n项和Sn=-44，求n的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=ex，g（x）=lnx+1，
    （1）求函数h（x）=f（x-1）-g（x）在区间[1，+∞）上的最小值；
    （2）已知1≤y＜x，求证：ex-y-1＞lnx-lny；
    （3）设H（x）=（x-1）2f（x），在区间（1，+∞）内是否存在区间[a，b]（a＞1），使函数H（x）在区间[a，b]的值域也是[a，b]？请给出结论，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．班主任为了对本班学生的考试成绩进行分析，决定从全班36名女同学，24名男同学中随机抽取一个容量为5的样本进行分析．
    （1）如果按性别比例分层抽样，可以得到多少个不同的样本？（只要求写出计算式即可）
    （2）随机抽取5位，他们的数学分数从小到大排序是：89，91，93，95，97，物理分数从小到大排序是：87，89，89，92，93
    ①若规定90分以上为优秀，求这5位同学中恰有2位同学的数学和物理分数均为优秀的概率；②若这5位同学的数学、物理分数事实上对应如表：
    学生编号12345
    数学分数x8991939597
    物理分数y8789899293
    根据上表数据，用变量y与x的相关系数或散点图说明物理成绩y与数学成绩x之间线性相关关系的强弱．如果具有较强的线性相关关系，求y与x的线性回归方程（系数精确到0.01）；如果不具有线性相关性，请说明理由．
    参考公式：相关系数r=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sqrt{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}\sum_{i=1}^{n}（{y}_{i}-\overline{y}）^{2}}}$；回归直线的方程是：$\stackrel{∧}{y}$=bx+a，其中对应的回归估计值b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，a=$\overline{y}$-b$\overline{x}$，$\stackrel{∧}{{y}_{i}}$是与xi对应的回归估计值．
    参考值：$\sqrt{15}$≈3.9．

    查看答案和解析>>

    同步练习册答案