
分析 (1)根据已知原函数的解析式求导,分析定义域内各区间上导函数的符号,进而可得f(x)的单调区间;
(2)存在x1,x2∈(1,+∞)且x1≠x2,使|f(x1)-f(x2)|≥k|lnx1-lnx2|成立,即存在x1,x2∈(1,+∞)且x1≠x2,使f(x2)+klnx2≥f(x1)+klnx1成立.令h(x)=f(x)+klnx,利用导数法求其最值,可得答案.
解答 解:(1)∵函数f(x)=$\frac{1+2lnx}{x^2}$.
∴$f'(x)=\frac{-4lnx}{x^3}$,
令f′(x)=0得x=1,
x∈(0,1)时,f′(x)>0,f(x)单调递增;x∈(1,+∞)时,f′(x)<0,f(x)单调递减;
综上,f(x)单调递增区间为(0,1),单调递减区间为(1,+∞).(4分)
(2)不妨设x1>x2>1,由(1)知x∈(1,+∞)时,f(x)单调递减.
|f(x1)-f(x2)|≥k|lnx1-lnx2|等价于f(x2)-f(x1)≥k(lnx1-lnx2),
即f(x2)+klnx2≥f(x1)+klnx1,
存在x1,x2∈(1,+∞)且x1≠x2,使f(x2)+klnx2≥f(x1)+klnx1成立.(7分)
令h(x)=f(x)+klnx,h(x)在(1,+∞)上存在减区间.$h'(x)=\frac{{k{x^2}-4lnx}}{x^3}<0$有解,即$k<\frac{4lnx}{x^2}$有解,即$k<{(\frac{4lnx}{x^2})_{max}}$.(9分)
令$t(x)=\frac{4lnx}{x^2}$,$t'(x)=\frac{4(1-2lnx)}{x^3}$,$x∈(0,\sqrt{e})$时,f'(x)>0,f(x)单调递增,$x∈(\sqrt{e},+∞)$时,f'(x)<0,f(x)单调递减,
∴${(\frac{4lnx}{x^2})_{max}}=\frac{2}{e}$,
∴$k<\frac{2}{e}$.(12分)
点评 本题考查的知识点是利用导数求闭区间上函数的最值,利用导数研究函数的单调性,难度中档.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{5}$]∪[7,+∞) | B. | [$\frac{1}{5}$,7] | C. | (-∞,$\frac{1}{7}$]∪[5,+∞) | D. | [$\frac{1}{7}$,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2520 | B. | 1440 | C. | -1440 | D. | -2520 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
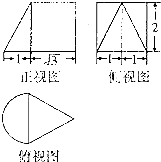
| A. | $\frac{π}{3}$+2$\sqrt{3}$ | B. | $\frac{π}{3}$+$\sqrt{3}$ | C. | π+2$\sqrt{3}$ | D. | $\frac{2π}{3}$+$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
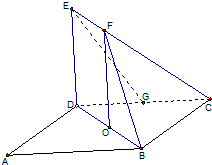 如图,菱形ABCD的中心为O,四边形ODEF为矩形,平面ODEF⊥平面ABCD,DE=DA=DB=2.
如图,菱形ABCD的中心为O,四边形ODEF为矩形,平面ODEF⊥平面ABCD,DE=DA=DB=2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com