
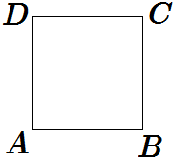
 �ʵ�P����ͼ���õ�������ABCD�Ķ���A���������������ӵ�������������µĹ����ڶ���������ƶ�������������ִ��ڵ���5����ƽ����AB�ߵķ����ƶ��������������С�ڵ���4����ƽ����AD�ߵķ����ƶ�����������2n��n��N*���κ��ʵ�P�ص�A��ĸ���Ϊan���ص�C��ĸ���Ϊcn��
�ʵ�P����ͼ���õ�������ABCD�Ķ���A���������������ӵ�������������µĹ����ڶ���������ƶ�������������ִ��ڵ���5����ƽ����AB�ߵķ����ƶ��������������С�ڵ���4����ƽ����AD�ߵķ����ƶ�����������2n��n��N*���κ��ʵ�P�ص�A��ĸ���Ϊan���ص�C��ĸ���Ϊcn������ �������������û����¼����ʼӷ���ʽ��������¼��˷���ʽ�����a1��
����X�Ŀ���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к���ѧ������
����m=2015ʱ���ܱȽ��ʵ�P�ص�A��ĸ��ʡ��ص�C��ĸ��ʺ�$\frac{1}{2}$�Ĵ�С��
��� �⣺����������${a}_{1}=\frac{1}{3}��\frac{1}{3}+\frac{2}{3}��\frac{2}{3}$=$\frac{5}{9}$��
����X�Ŀ���ȡֵΪ0��1��2��
P��X=0��=��$\frac{1}{3}$��4+��$\frac{2}{3}$��4+2����$\frac{1}{3}$��2����$\frac{2}{3}$��2=$\frac{25}{81}$��
P��X=1��=$4����\frac{2}{3}��^{2}����\frac{1}{3}��^{2}$+2��$��\frac{2}{3}��^{3}��\frac{1}{3}+2����\frac{2}{3}������\frac{1}{3}��^{3}$=$\frac{36}{81}$��
P��X=2��=$2����\frac{2}{3}��^{3}��\frac{1}{3}+2����\frac{2}{3}������\frac{1}{3}��^{3}$=$\frac{20}{81}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{25}{81}$ | $\frac{36}{81}$ | $\frac{20}{81}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��С���ѧ���������ǻ����⣬����ʱҪ�������⣬ע�⻥���¼����ʼӷ���ʽ��������¼��˷���ʽ�ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� | �Ŀ� | �ϼ� | |
| �� | 18 | 9 | |
| Ů | 8 | 15 | |
| �ϼ� |
| P��K2��k0�� | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�$\frac{1}{5}$]��[7��+�ޣ� | B�� | [$\frac{1}{5}$��7] | C�� | ��-�ޣ�$\frac{1}{7}$]��[5��+�ޣ� | D�� | [$\frac{1}{7}$��5] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2520 | B�� | 1440 | C�� | -1440 | D�� | -2520 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9 | B�� | -9 | C�� | 0 | D�� | 1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com