
 (e为自然对数的底数),当a>0时,讨论函数g(x)是否存在不动点,若存在求出a的范围,若不存在说明理由.
(e为自然对数的底数),当a>0时,讨论函数g(x)是否存在不动点,若存在求出a的范围,若不存在说明理由.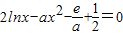 有解,利用导数法求出
有解,利用导数法求出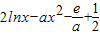 的最值,比较后可得结论.
的最值,比较后可得结论.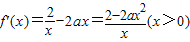
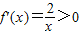 ,f(x)在(0,+∞)上位增函数,无极值;
,f(x)在(0,+∞)上位增函数,无极值;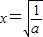 ,列表如下:
,列表如下:| X | 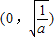 | 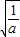 |  |
| f'(x) | + | _ | |
| f(x) | 增 | 极大值 | 减 |
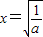 时,f(x)有极大值=
时,f(x)有极大值=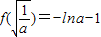
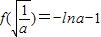 .┅┅(10分)
.┅┅(10分)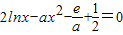 有解.
有解.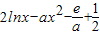 ,(a>0)有(2)可知h(x)极大值=
,(a>0)有(2)可知h(x)极大值=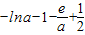 =
=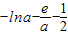 ,下面判断h(x)极大值是否大于0,设
,下面判断h(x)极大值是否大于0,设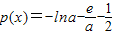 ,(a>0),
,(a>0), ,列表如下:
,列表如下:| A | (0,e)) | e | (e,+∞) |
| p'(a) | + | - | |
| P(a) | 增 | 极大值 | 减 |
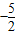 <0,所以
<0,所以 恒成立,即h(x)极大值小于零,所以g(x)无不动点.┅┅(14分)
恒成立,即h(x)极大值小于零,所以g(x)无不动点.┅┅(14分)

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
| π |
| 2 |
| π |
| 2 |
| 1 |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省六安市徐集中学高三(上)摸底数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省六安市徐集中学高三(上)摸底数学试卷(文科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆十一中高一(上)数学单元测试10(集合到等比数列)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省上饶市重点中学高三第二次联考数学试卷(文科)(解析版) 题型:解答题
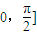 的函数f(x)=sinx,若
的函数f(x)=sinx,若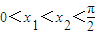 ,则必存在x∈(x1,x2),使(x1-x2)cosx=sinx1-sinx2成立;
,则必存在x∈(x1,x2),使(x1-x2)cosx=sinx1-sinx2成立; 成立的概率是
成立的概率是 ;
;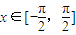 ,若f(x1)>f(x2),则不等式x12>x22必定成立.
,若f(x1)>f(x2),则不等式x12>x22必定成立.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com