
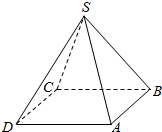
 如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为$\sqrt{7}$m,求证:
如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为$\sqrt{7}$m,求证:分析 (1)连接AC和BD交于O,连接SO.作SP⊥AB,连接OP.在Rt△SOP中,SO=$\sqrt{7}$(m),OP=$\frac{1}{2}$BC=1,所以SP=2$\sqrt{2}$,由此能求出制造这个塔顶需要多少铁板.
(2)利用棱锥的体积公式,即可得出结论.
解答  解:(1)如图所示,连接AC和BD交于O,连接SO.作SP⊥AB,连接OP.
解:(1)如图所示,连接AC和BD交于O,连接SO.作SP⊥AB,连接OP.
在Rt△SOP中,SO=$\sqrt{7}$(m),OP=$\frac{1}{2}$BC=1(m),
所以SP=2$\sqrt{2}$(m),
则△SAB的面积是$\frac{1}{2}$×2×2$\sqrt{2}$=2$\sqrt{2}$(m2).
所以四棱锥的侧面积是4×2$\sqrt{2}$=8$\sqrt{2}$(m2),
即制造这个塔顶需要8$\sqrt{2}$m2铁板.
(2)铁塔的体积V=$\frac{1}{3}×2×2×\sqrt{7}$=$\frac{4\sqrt{7}}{3}$m3.
点评 本题考查四棱锥的侧面积、体积的应用,考查空间思维能力和空间想象能力,考查学生的计算能力,属于中档题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 点P(0,0)为曲线C:y=x3的“相似拐点” | |
| B. | 点P(0,0)为曲线C:y=sinx的“相似拐点” | |
| C. | 点P(0,0)为曲线C:y=tanx的“相似拐点” | |
| D. | 点P(1,0)为曲线C:y=lnx的“相似拐点” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com