
 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式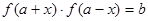 对定义域中的每一个
对定义域中的每一个 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.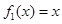 是否为“(
是否为“( )型函数”,并说明理由;
)型函数”,并说明理由; 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对 ;
;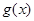 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对 为(1,4).当
为(1,4).当 时,
时,

 ,若当
,若当 时,都有
时,都有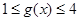 ,试求
,试求 的取值范围.
的取值范围.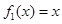 不是“(
不是“( )型函数”,理由详见解析;(2)
)型函数”,理由详见解析;(2) (答案不唯一)(3)
(答案不唯一)(3)
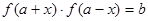 展开后的方程中如果不含x说明对任意x都成立,则函数
展开后的方程中如果不含x说明对任意x都成立,则函数 是“(
是“( )型函数”,如果展开后的方程含x,则根据方程只能求出某个或某些x满足要求而不是每一个x都符合,则函数
)型函数”,如果展开后的方程含x,则根据方程只能求出某个或某些x满足要求而不是每一个x都符合,则函数 不是“(
不是“( )型函数(Ⅱ)根据定义列出方程,满足方程的实数对应有无数对,只取其中一对就可以。(Ⅲ)难度系数较大,应先根据题意分析出当
)型函数(Ⅱ)根据定义列出方程,满足方程的实数对应有无数对,只取其中一对就可以。(Ⅲ)难度系数较大,应先根据题意分析出当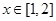 时,
时,  ,此时
,此时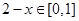 。根据已知
。根据已知 时,
时, ,其对称轴方程为
,其对称轴方程为 。属动轴定区间问题需分类讨论,在每类中得出
。属动轴定区间问题需分类讨论,在每类中得出 时
时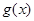 的值域即
的值域即 的值域,从而得出
的值域,从而得出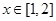 时
时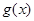 的值域,把两个值域取并集即为
的值域,把两个值域取并集即为 的
的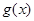 的值域,由
的值域,由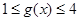 可知
可知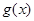 的值域是
的值域是 的子集,列出关于m的不等式即可求解。
的子集,列出关于m的不等式即可求解。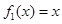 不是“(
不是“( )型函数”,因为不存在实数对
)型函数”,因为不存在实数对 使得
使得 ,
, 对定义域中的每一个
对定义域中的每一个 都成立;
都成立; ,得
,得 ,所以存在实数对,
,所以存在实数对, ,使得
,使得 对任意的
对任意的 都成立;
都成立;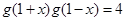 ,所以当
,所以当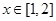 时,
时,  ,其中
,其中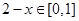 ,而
,而 时,
时, ,其对称轴方程为
,其对称轴方程为 .
. ,即
,即 时,
时,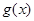 在
在 上的值域为
上的值域为 ,即
,即 ,则
,则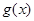 在
在 上 的值域为
上 的值域为 ,由题意得
,由题意得 ,从而
,从而 ;
;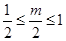 ,即
,即 时,
时,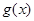 的值域为
的值域为 ,即
,即 ,则
,则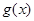 在
在 上的值域为
上的值域为 ,则由题意,得
,则由题意,得
 ,解得
,解得 ;
; ,即
,即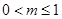 时,
时,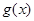 的值域为
的值域为 ,即
,即 ,则
,则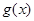 在
在 上的值域为
上的值域为 ,即
,即 ,则
,则 ,解得
,解得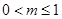 .
. 的取值范围是
的取值范围是 .
.

科目:高中数学 来源:不详 题型:解答题
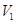 .
.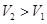 吗?若能、给出你的一种设计方案。
吗?若能、给出你的一种设计方案。 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
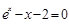 的一个根所在的区间是( )
的一个根所在的区间是( )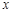 | -1 | 0 | 1 | 2 | 3 |
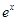 | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
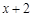 | 1 | 2 | 3 | 4 | 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com