
 ,符号
,符号 表示不超过
表示不超过 的最大整数,若关于
的最大整数,若关于 的方程
的方程 (
(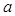 为常数)有且仅有3个不等的实根,则
为常数)有且仅有3个不等的实根,则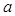 的取值范围是( ).
的取值范围是( ). A. | B. |
C. | D. |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:不详 题型:解答题
 ,若存在实数对(
,若存在实数对( ),使得等式
),使得等式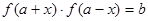 对定义域中的每一个
对定义域中的每一个 都成立,则称函数
都成立,则称函数 是“(
是“( )型函数”.
)型函数”.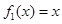 是否为“(
是否为“( )型函数”,并说明理由;
)型函数”,并说明理由; 是“(
是“( )型函数”,求出满足条件的一组实数对
)型函数”,求出满足条件的一组实数对 ;
;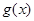 是“(
是“( )型函数”,对应的实数对
)型函数”,对应的实数对 为(1,4).当
为(1,4).当 时,
时,

 ,若当
,若当 时,都有
时,都有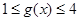 ,试求
,试求 的取值范围.
的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,如果每年平均增长5﹪,经过
,如果每年平均增长5﹪,经过 年,树林中有木材
年,树林中有木材
 ,
, (
( )与
)与 之间的函数关系式。
之间的函数关系式。 ?(结果保留一个有效数字)
?(结果保留一个有效数字) ,
, )
)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 的正方形
的正方形 ,点
,点 分别在边
分别在边 和
和 上,△
上,△ ,△
,△ 和四边形
和四边形 均由单一材料制成,制成△
均由单一材料制成,制成△ ,△
,△ 和四边形
和四边形 的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形
的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形 .则当
.则当
 时,定制这批地砖所需的材料费用最省?
时,定制这批地砖所需的材料费用最省?
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 关于时间
关于时间 的函数关系式分别为
的函数关系式分别为 ,
, ,
, ,
, ,有以下结论:
,有以下结论: 时,甲走在最前面;
时,甲走在最前面; 时,乙走在最前面;
时,乙走在最前面; 时,丁走在最前面,当
时,丁走在最前面,当 时,丁走在最后面;
时,丁走在最后面;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com