练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知三角形ABC的三个顶点的直角坐标分别为A（4，3）、B（0，0）、C（c，0）
    （1）若c=5，求sin∠A的值；
    （2）若∠A为钝角，求c的取值范围．
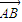
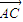
    【答案】分析：（1） 题目中给出三角形ABC的三个顶点的坐标，可以得到向量，的坐标，进而可求得向量的夹角，所以欲求sin∠A的值，
    根据向量的夹角公式，可以先求cos∠A的值；
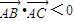
    （2）若∠A为钝角，则有cos∠A＜0且cos∠A≠-1．其中cos∠A＜0转化为，可得关于c的关系式，解可得答案．
    解答：解：（1），，
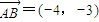
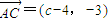
    若c=5，则，
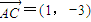
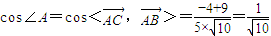
    ∴，（4分）
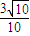
    ∴sin∠A=；（6分）
    （2）若∠A为钝角，则
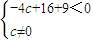
    解得，（11分）
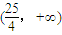
    ∴c的取值范围是（12分）
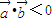
    点评：本题容易忽视了两向量共线且反向时，此时的夹角为180．两非零向量 的夹角为钝角的充要条件是且 它们不平行．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知三角形ABC的三个内角A，B，C成等差数列，且AB=1，BC=4，则中线AD的长为
    A、
    		3
    B、1
    C、
    		2
    D、
    		3
    +
    		2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知三角形△ABC的三个顶点是A（4，0），B（6，7），C（0，8）．
    （1）求BC边上的高所在直线的方程；
    （2）求BC边上的中线所在直线的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•湛江二模）已知三角形ABC的三个顶点的坐标分别为A（3，2），B（1，3），C（2，5），l为BC边上的高所在直线．
    （1）求直线l的方程；
    （2）直线l与椭圆
    x2
    a2
    +
    y2
    b2
    =1    相交于D、E两点，△CDE是以C（2，5）为直角顶点的等腰直角三角形，求该椭圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知三角形ABC的三个内角A，B，C所对的边长分别为a，b，c，且b2+c2-bc=a2；
    c
    b
    =
    1
    2
    +
    		3
    ．则tanB=
    1
    2
    1
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知三角形ABC的三个顶点是A（4，0），B（6，7），C（0，3），求：
    （1）求BC边上的中线所在直线的方程；
    （2）求BC边的垂直平分线的方程．

    查看答案和解析>>

    同步练习册答案