
(本小题满分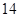 分)设函数
分)设函数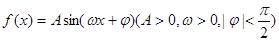 的最高点
的最高点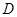 的坐标为(
的坐标为(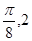 ),由最高点
),由最高点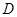 运动到相邻最低点时,函数图形与
运动到相邻最低点时,函数图形与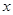 的交点的坐标为(
的交点的坐标为(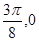 ).
).
(1)求函数 的解析式.
的解析式.
(2)当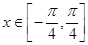 时,求函数
时,求函数 的最大值和最小值以及分别取得最大值和最小值时
的最大值和最小值以及分别取得最大值和最小值时
相应的自变量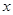 的值.
的值.
(3)将函数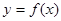 的图象向右平移
的图象向右平移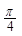 个单位,得到函数
个单位,得到函数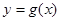 的图象,求函数
的图象,求函数
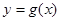 的单调减区间.
的单调减区间.
(1)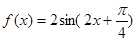
(2)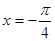 时,函数
时,函数 取得最小值
取得最小值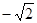 ;
;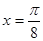 时,函数
时,函数 取得最大值
取得最大值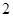
(3)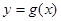 的单调减区间为
的单调减区间为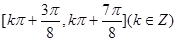
【解析】
试题分析:(1)∵由最高点D(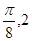 )运动到相邻最低点时,函数图形与
)运动到相邻最低点时,函数图形与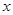 的交点的坐标
的交点的坐标
为(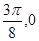 ),
),
∴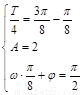 , ……2分
, ……2分
从而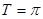 ,
,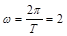 ,
,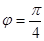 , ……4分
, ……4分
∴函数解析式为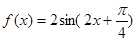 . ……5分
. ……5分
(2)由(1)得函数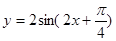 ,
,
当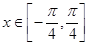 时,
时,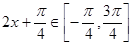 . ……6分
. ……6分
∴当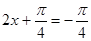 ,即
,即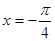 时,函数
时,函数 取得最小值
取得最小值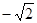 . ……8分
. ……8分
当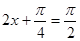 ,即
,即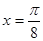 时,函数
时,函数 取得最大值
取得最大值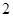 .
……10分
.
……10分
(3)由题意得,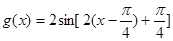 ,即
,即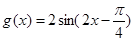 , ……12分
, ……12分
由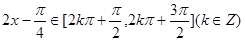 ,
,
得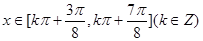 , ……13分
, ……13分
即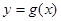 的单调减区间为
的单调减区间为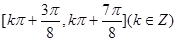 . ……14分
. ……14分
考点:本小题主要考查由三角函数的图象求函数的解析式以及对函数性质如最值、单调区间等的研究,考查学生数形结合思想的应用.
点评:一般来说,由三角函数图象确定解析式时,由最值确定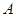 ,由周期确定
,由周期确定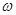 ,由特殊值确定
,由特殊值确定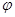 ,知道了函数解析式,求函数的最值和单调区间时要借助三角函数的图象解决问题.
,知道了函数解析式,求函数的最值和单调区间时要借助三角函数的图象解决问题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2011-2012学年内蒙古呼伦贝尔市高三第四次模拟考试理科数学试卷 题型:解答题
(本小题满分12分)
已知函 的部分图象如图所示:
的部分图象如图所示:
(1)求 的值;
的值;
(2)设 ,当
,当 时,求函数
时,求函数 的值域.
的值域.

查看答案和解析>>
科目:高中数学 来源:2008年普通高等学校招生全国统一考试理科数学(重庆卷) 题型:解答题
(本小题满分13分.(Ⅰ)小问5分.(Ⅱ)小问8分.)
设函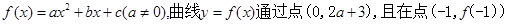
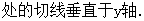
(Ⅰ)用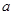 分别表示
分别表示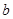 和
和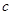 ;
;
(Ⅱ)当bc取得最小值时,求函数g(x)=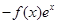 的单调区间。
的单调区间。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年重庆卷理)(本小题满分13分.(Ⅰ)小问5分.(Ⅱ)小问8分.)
设函![]()
![]()
(Ⅰ)用![]() 分别表示
分别表示![]() 和
和![]() ;
;
(Ⅱ)当bc取得最小值时,求函数g(x)=![]() 的单调区间。
的单调区间。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com