
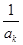 ,
,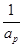 ,
,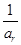 成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.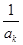 ,
,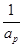 ,
,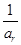 成等差数列,则
成等差数列,则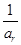 =
=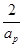 -
-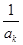 =
=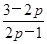 .因为p≥2,所以ar<0与数列{an}为正数相矛盾,因此,当k=1时不存在;
.因为p≥2,所以ar<0与数列{an}为正数相矛盾,因此,当k=1时不存在;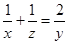 ,所以z=
,所以z=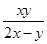 .令y=2x-1,得z=xy=x(2x-1),此时ak=x=2k-1,ap=y=2x-1=2(2k-1)-1,所以p=2k-1,ar=z=(2k-1)(4k-3)=2(4k2-5k+2)-1,所以r=4k2-5k+2.
.令y=2x-1,得z=xy=x(2x-1),此时ak=x=2k-1,ap=y=2x-1=2(2k-1)-1,所以p=2k-1,ar=z=(2k-1)(4k-3)=2(4k2-5k+2)-1,所以r=4k2-5k+2.

科目:高中数学 来源:不详 题型:解答题
 ,n∈N*,其中c为实数.
,n∈N*,其中c为实数.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
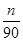 (21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.
(21n-n2-5)(n=1,2,…,12),按此预测,在本年度内,需求量超过1.5万件的月份是________.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com