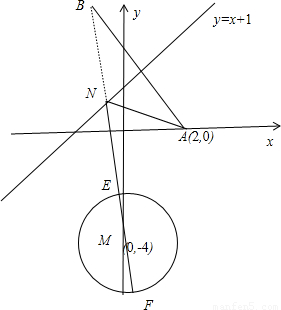
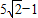一束光线从光源A(2,0)射到直线y=x+1上,经过反射,最后反射光线射到圆C1:x2+y2+8y+15=0上,求光线传播到圆的最短路径长为 .
【答案】
分析:设A关于y=x+1的对称点为B,由对称性可知AN=BN,所求光线传播到圆的路径长AN+NE=BN+NE,要使得其最小,则BE过圆心M(0,-4)时满足条件,根据两点间的距离公式可求
解答:解:如图所示,设A关于y=x+1的对称点为B,则可得B(-1,3),由对称性可知AN=BN
所求光线传播到圆的路径长AN+NE=BN+NE,要使得其最小,则BE过圆心M(0,-4)时满足条件
而BE=BM-ME=
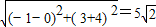
-1
故答案为:
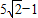
 点评:
点评:本题主要考查了利用点与点关于直线对称问题求解距离的最小值,解题的关键是要能够发现A关于已知直线的对称点B之后可知AN=BN,从而问题转化为求解在圆外一点B,使得点B到圆上一点的距离最小(大)

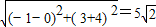 -1
-1