
 已知某空间几何体的三视图如图所示,若三个正方形的边长均为2,则该几何体的表面积为( )
已知某空间几何体的三视图如图所示,若三个正方形的边长均为2,则该几何体的表面积为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | 8$\sqrt{3}$ | D. | 12+4$\sqrt{3}$ |
分析 由题意和三视图知:由两种情况,
(1)该几何体是棱长为2正方体截去一个三棱锥所得的组合体,由正方体的性质判断出各个面的形状,由直观图和三角形的面积公式求出该几何体的表面积;
(2)该几何体是边长为2的正方体被两个平行平面所截后的几何体,由正方体的性质判断出各个面的形状,由直观图和三角形的面积公式求出该几何体的表面积.
解答 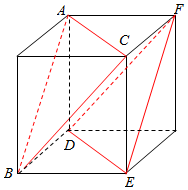 解:由题意和三视图知:由两种情况,
解:由题意和三视图知:由两种情况,
(1)该几何体是棱长为2正方体截去一个三棱锥所得的组合体,
截面△ABC是等边三角形,边长是2$\sqrt{2}$,
∴该几何体的表面积S=$3×2×2+3×\frac{1}{2}×2×2+\frac{\sqrt{3}}{4}×{(2\sqrt{2})}^{2}$
=18+2$\sqrt{3}$
由三个视图均为边长为2的正方形,故正方体的棱长为2
(2)几何体是边长为2的正方体被两个平行平面所截后的几何体,
根据三视图画出直观图:
截面△ABC和△DEF是全等的等边三角形,且边长是2$\sqrt{2}$,
由图得,该几何体表面有:
6个全等的等腰直角三角形、直角边是2,截面△ABC和△DEF构成,
∴该几何体的表面积S=$6×\frac{1}{2}×2×2$+2×$\frac{\sqrt{3}}{4}×{(2\sqrt{2})}^{2}$=12+4$\sqrt{3}$
综上可得,该几何体的表面积为18+2$\sqrt{3}$或12$+4\sqrt{3}$,
故选:D.
点评 本题考查由三视图求几何体的表面积,在三视图与直观图转化过程中,以一个正方体为载体是很好的方式,使得作图更直观,考查空间想象能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
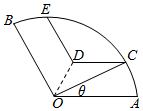 如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.
如图,扇形AOB是一个植物园的平面示意图,其中∠AOB=$\frac{2π}{3}$,半径OA=OB=1km,为了便于游客观赏,拟在圆内铺设一条从入口A到出口B的观赏道路,道路由弧$\widehat{AC}$,线段CD,线段DE和弧$\widehat{EB}$组成,且满足:$\widehat{AC}$=$\widehat{EB}$,CD∥AO.DE∥OB,OD∈[$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{6}}{3}$](单位:km),设∠AOC=θ.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知长方形ABCD中,AB=1,AD=$\sqrt{2}$,现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.
已知长方形ABCD中,AB=1,AD=$\sqrt{2}$,现将长方形沿对角线BD折起,使AC=a,得到一个四面体A-BCD,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
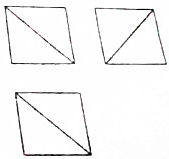 如图,粗线画出的是一个正方体被两个平行平面所截后的几何体的三视图,图中三个正方形的边长为4,则此几何体的表面积为( )
如图,粗线画出的是一个正方体被两个平行平面所截后的几何体的三视图,图中三个正方形的边长为4,则此几何体的表面积为( )| A. | 40+8$\sqrt{3}$ | B. | 48+8$\sqrt{3}$ | C. | 40+16$\sqrt{3}$ | D. | 48+16$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∁UN∩M=∅ | B. | ∁UM∩N=∅ | C. | ∁UM∩∁UN=∅ | D. | ∁UM∪∁UN=∅ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com