
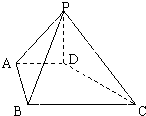
【题目】如图,PD⊥平面ABCD,DC⊥AD,BC∥AD,PD:DC:BC=1:1: ![]() .
. 
(1)若AD=DC,求异面直线PA,BC所成的角;
(2)求PB与平面PDC所成角大小;
(3)求二面角D﹣PB﹣C的正切值.
【答案】
(1)解:由已知得异面直线PA,BC所成的角为直线PA与AD所成的角为∠PAD=45°
(2)解:由已知得BC与平面PDC垂直,所以PB与平面PDC所成角为∠CPB=45°
(3)解:取PC中点E,连接DE,则DE⊥PC
由于BC⊥平面PDC,所以PBC⊥平面PDC,从而DE⊥平面C,做EF⊥PB于点F,连接DF,可得DF⊥PB
所以∠DFE为二面角D﹣PB﹣C的平面角.
计算可得DE= ![]() ,EF=
,EF= ![]() .
.
所以二面角D﹣PB﹣C的正切值为 ![]() .
.
【解析】(1)根据异面直线所成角的定义进行求解,(2)根据直线和平面所成角的定义进行求解,(3)根据二面角的定义作出二面角的平面角进行求解.
【考点精析】关于本题考查的异面直线及其所成的角和空间角的异面直线所成的角,需要了解异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则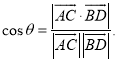 才能得出正确答案.
才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() +
+ ![]() )x3(a>0且a≠1).
)x3(a>0且a≠1).
(1)求函数f(x)的定义域;
(2)讨论函数f(x)的奇偶性;
(3)求a的取值范围,使f(x)>0在定义域上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=AD=CD=1,BD= ![]() ,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′﹣BCD,使平面A′BD⊥平面BCD,则下列结论正确的是( )
,BD⊥CD.将四边形ABCD沿对角线BD折成四面体A′﹣BCD,使平面A′BD⊥平面BCD,则下列结论正确的是( ) 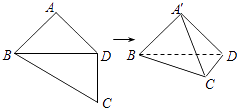
A.A′C⊥BD
B.∠BA′C=90°
C.CA′与平面A′BD所成的角为30°
D.四面体A′﹣BCD的体积为 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在[﹣1,1]上的奇函数,且f(1)=1,若m,n∈[﹣1,1],m+n≠0时,有 ![]() >0.
>0.
(Ⅰ)证明f(x)在[﹣1,1]上是增函数;
(Ⅱ)解不等式f(x2﹣1)+f(3﹣3x)<0
(Ⅲ)若f(x)≤t2﹣2at+1对x∈[﹣1,1],a∈[﹣1,1]恒成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点,焦点F1 , F2在坐标轴上,离心率为 ![]() ,且过点(4,﹣
,且过点(4,﹣ ![]() ),点M(3,m)在双曲线上.
),点M(3,m)在双曲线上.
(1)求双曲线方程;
(2)求证:MF1⊥MF2;
(3)求△F1MF2的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x取实数,则f(x)与g(x)表示同一个函数的是( )
A.f(x)=x,g(x)= ![]()
B.f(x)= ![]() ,g(x)=
,g(x)= ![]()
C.f(x)=1,g(x)=(x﹣1)0
D.f(x)= ![]() ,g(x)=x﹣3
,g(x)=x﹣3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆 ![]() 的离心率为
的离心率为 ![]() ,右焦点到直线
,右焦点到直线 ![]() 的距离为
的距离为 ![]() ,过M(0,﹣1)的直线l交椭圆于A,B两点.
,过M(0,﹣1)的直线l交椭圆于A,B两点.
(1)求椭圆的方程;
(2)若直线l交x轴于N, ![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com