
 ,点N到直线PM的距离为1,求直线PN的方程.
,点N到直线PM的距离为1,求直线PN的方程.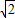 ,可得
,可得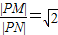 ,结合两点间的距离,化简整理得x2+y2-6x+1=0,又由点N到PM的距离为1,即|MN|=2,可得直线PM的斜率,进而可得直线PM的方程,并将方程代入x2+y2-6x+1=0整理得x2-4x+1=0,解可得x的值,进而得P的坐标,由直线的方程代入点的坐标可得答案.
,结合两点间的距离,化简整理得x2+y2-6x+1=0,又由点N到PM的距离为1,即|MN|=2,可得直线PM的斜率,进而可得直线PM的方程,并将方程代入x2+y2-6x+1=0整理得x2-4x+1=0,解可得x的值,进而得P的坐标,由直线的方程代入点的坐标可得答案.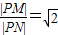 ,
, ,
,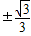
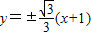
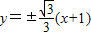 代入x2+y2-6x+1=0整理得x2-4x+1=0
代入x2+y2-6x+1=0整理得x2-4x+1=0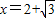 ,
,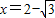
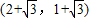 或
或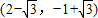
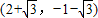 或
或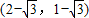


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源:2003-2004学年广东省广州市黄埔区高二数学竞赛试卷(解析版) 题型:解答题
 ,点N到直线PM的距离为1,求直线PN的方程.
,点N到直线PM的距离为1,求直线PN的方程.查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:7.6 直线与圆的位置关系(解析版) 题型:解答题
 ,点N到直线PM的距离为1,求直线PN的方程.
,点N到直线PM的距离为1,求直线PN的方程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com