
椭圆 :
: 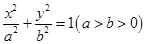 的左、右焦点分别是
的左、右焦点分别是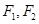 ,离心率为
,离心率为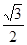 ,过
,过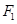 且垂直于
且垂直于 轴的直线被椭圆
轴的直线被椭圆 截得的线段长为
截得的线段长为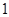 。
。
(Ⅰ)求椭圆 的方程;
的方程;
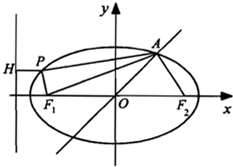
(Ⅱ)点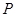 是椭圆
是椭圆 上除长轴端点外的任一点,连接
上除长轴端点外的任一点,连接 ,设
,设 的角平分线
的角平分线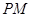 交
交 的长轴于点
的长轴于点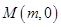 ,求
,求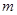 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,过点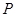 作斜率为
作斜率为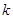 的直线
的直线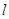 ,使
,使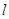 与椭圆
与椭圆 有且只有一个公共点,设直线的
有且只有一个公共点,设直线的 斜率分别为
斜率分别为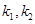 。若
。若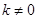 ,试证明
,试证明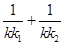 为定值,并求出这个定值。
为定值,并求出这个定值。
(Ⅰ)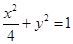 (Ⅱ)
(Ⅱ)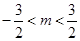 (Ⅲ)
(Ⅲ)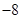
【解析】(Ⅰ)设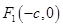 ,过
,过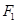 且垂直于
且垂直于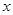 轴的直线与椭圆相交,则其中的一个交点坐标为
轴的直线与椭圆相交,则其中的一个交点坐标为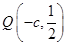 ,由题意可得
,由题意可得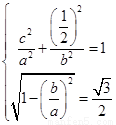 解得
解得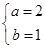 ,
,
所以椭圆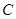 的方程为
的方程为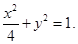
(Ⅱ)由(Ⅰ)知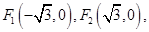 则
则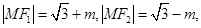
由椭圆定义得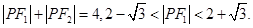
因为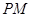 平分
平分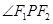 ,
,
所以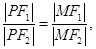
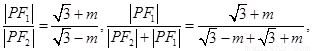
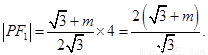
所以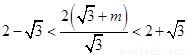 ,
,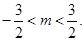
另解:由题意可知: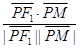 =
=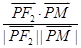 ,
,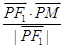 =
=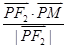 ,
,
设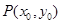 其中
其中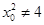 ,将向量坐标代入并化简得
,将向量坐标代入并化简得
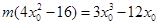 ,因为
,因为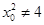 ,
,
所以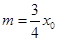 ,而
,而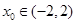 ,所以
,所以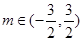 .
.
(Ⅲ)因为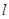 与椭圆
与椭圆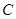 有且只有一个公共点,则点
有且只有一个公共点,则点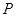 为切点,设
为切点,设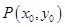
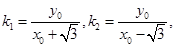
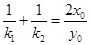 .
.
设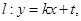 与
与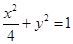 联立得
联立得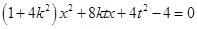 ,
,
由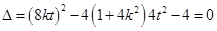 得
得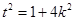 ,
,
所以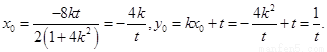
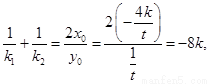
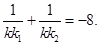
另解:由题意可知,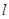 为椭圆的在
为椭圆的在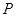 点处的切线,由导数法可求得,切线方程
点处的切线,由导数法可求得,切线方程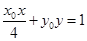 ,
,
所以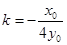 ,而
,而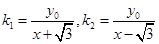 ,代入
,代入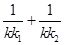 中得
中得
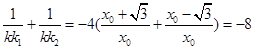 为定值.
为定值.
【考点定位】本题通过椭圆的离心率、焦点、弦长、定义等基本知识来考查运算能力、推理论证能力。第一问较为简单,通过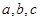 三者的固有关系确定椭圆方程为
三者的固有关系确定椭圆方程为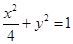 .第二问处理方式很多,可利用角平分线性质定理寻找线段间的比例关系、可利用点
.第二问处理方式很多,可利用角平分线性质定理寻找线段间的比例关系、可利用点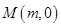 到直线
到直线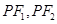 的距离相等来确定
的距离相等来确定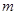 的取值范围,但要注意直线斜率不存在的情形的说明.第三问中的直线
的取值范围,但要注意直线斜率不存在的情形的说明.第三问中的直线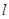 的方程设法很多,也是决定运算量大小的关键,如果设为
的方程设法很多,也是决定运算量大小的关键,如果设为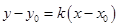 ,则会出现
,则会出现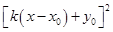 ,其运算强度较大,而设为
,其运算强度较大,而设为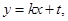 可通过
可通过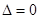 得到关系式
得到关系式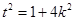 ,大大简化了运算.
,大大简化了运算.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 6 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知点P在椭圆C:
已知点P在椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
| GM |
| GN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 3 |
| ||
| 2 |
| 10 |
| 3 |
| 1 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| 1-a2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com