
在四棱锥P-ABCD中,AB∥DC,AB⊥平面PAD, PD=AD,AB=2DC,E是PB的中点.

求证:(1)CE∥平面PAD;
(2)平面PBC⊥平面PAB.
(1)详见解析; (2)详见解析.
【解析】
试题分析:(1)要证明线面平行根据线面平行的判定定理可将问题转化为证明平面外直线平行与平面内一条直线,则此问题关键即为找出这条直线,又由题中所给:AB=2DC,E是PB的中点,不难想到取PA的中点,进而运用三角形的中位线构造平行关系,问题即可得证; (2)中要证明面面垂直由面面垂直的判定定理可知将问题转化为证明线面垂直,结全题中所给条件和(1)中已证明的过程,不难发现可转化为去证: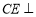 平面PAB,再根据线面垂直的判定定理可转化为证线线垂直:
平面PAB,再根据线面垂直的判定定理可转化为证线线垂直: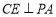 ,
,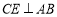 ,这样问题即可得证.
,这样问题即可得证.
试题解析:(1)取PA的中点F,连EF,DF. 2分
因为E是PB的中点,所以EF // AB,且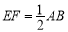 .
.
因为AB∥CD,AB=2DC,所以EF∥CD, 4分
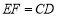 ,于是四边形DCEF是平行四边形,
,于是四边形DCEF是平行四边形,
从而CE∥DF,而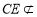 平面PAD,
平面PAD,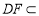 平面PAD,
平面PAD,
故CE∥平面PAD. 7分
(2)因为PD=AD,且F是PA的中点,所以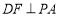 .
.
因为AB⊥平面PAD,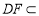 平面PAD,所以
平面PAD,所以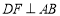 . 10分
. 10分
因为CE∥DF,所以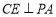 ,
,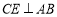 .
.
因为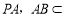 平面PAB,
平面PAB, ,所以
,所以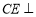 平面PAB.
平面PAB.
因为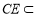 平面PBC,所以平面PBC⊥平面PAB. 14分
平面PBC,所以平面PBC⊥平面PAB. 14分
考点:1.线线,线面平行的转化;2.线线,线面,面面垂直的转化


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:高中数学 来源:2013-2014学年江苏省高考模拟考试文科数学试卷(解析版) 题型:解答题
数列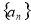 满足:
满足: ,
,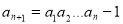 (
(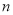 ≥3),记
≥3),记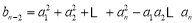
(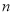 ≥3).
≥3).
(1)求证数列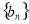 为等差数列,并求通项公式;
为等差数列,并求通项公式;
(2)设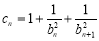 ,数列{
,数列{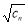 }的前n项和为
}的前n项和为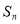 ,求证:
,求证: <
<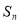 <
<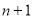 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三第二次调研测试数学试卷(解析版) 题型:解答题
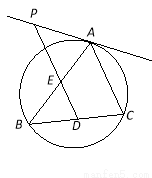
如图,△ABC内接于圆O,D为弦BC上一点,过D作直线DP // AC,交AB于点E,交圆O
在A点处的切线于点P.求证:△PAE∽△BDE.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三第二次调研测试数学试卷(解析版) 题型:填空题
设x,y,z是实数,9x,12y,15z成等比数列,且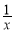 ,
,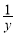 ,
,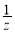 成等差数列,则
成等差数列,则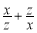 的值是 .
的值是 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三第二次调研测试数学试卷(解析版) 题型:填空题
从编号为0,1,2, ,79的80件产品中,采用系统抽样的方法抽取容量是5的样本,若编号为28的产品在样本中,则该样本中产品的最大编号为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南通市高三年级第三次模拟考试理科数学试卷(解析版) 题型:填空题
设数列{an}为等差数列,数列{bn}为等比数列.若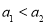 ,
,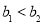 ,且
,且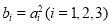 ,则
,则
数列{bn}的公比为 .
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省南京市高三年级第三次模拟考试数学试卷(解析版) 题型:填空题
已知椭圆C: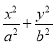 =1(a>b>0)过点P(-1,-1),c为椭圆的半焦距,且c=
=1(a>b>0)过点P(-1,-1),c为椭圆的半焦距,且c= b.过点P作两条互相垂直的直线l1,l2与椭圆C分别交于另两点M,N.
b.过点P作两条互相垂直的直线l1,l2与椭圆C分别交于另两点M,N.
(1)求椭圆C的方程;
(2)若直线l1的斜率为-1,求△PMN的面积;
(3)若线段MN的中点在x轴上,求直线MN的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com