
经过原点的直线与椭圆
交于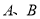
两点,点
为椭圆上不同于
的一点,直线
的斜率均存在,且直线
的斜率之积为
.
(1)求椭圆
的离心率;
(2)设
分别为椭圆的左、右焦点,斜率为
的直线
经过椭圆的右焦点,且与椭圆交于
两点.若点
在以
为直径的圆内部,求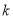
的取值范围.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:2016-2017学年云南省高二上学期期末考试数学(理)试卷(解析版) 题型:选择题
高二某班共有学生56人,座号分别为1,2,3,…,56,现根据座号,用系统抽样的方法,抽取一个容量为4的样本.已知4号、18号、46号同学在样本中,那么样本中还有一个同学的座号是( )
A. 30 B. 31 C. 32 D. 33
查看答案和解析>>
科目:高中数学 来源:2017届河北省石家庄市高三第二次质量检测数学(理)试卷(解析版) 题型:选择题
若 ,则在
,则在 的展开式中,
的展开式中,  的幂函数不是整数的项共有( )
的幂函数不是整数的项共有( )
A. 13项 B. 14项 C. 15项 D. 16项
查看答案和解析>>
科目:高中数学 来源:2017届河北省石家庄市高三第二次质量检测数学(理)试卷(解析版) 题型:选择题
在复平面中,复数 对应的点在 ( )
对应的点在 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:高中数学 来源:2017届贵州省贵阳市高三2月适应性考试(一)数学理试卷(解析版) 题型:填空题
我国古代数学家刘徽是公元三世纪世界上最杰出的数学家,他在《九章算术圆田术》注中,用割圆术证明了圆面积的精确公式,并给出了计算圆周率的科学方法.所谓“割圆术”,即通过圆内接正多边形细割圆,并使正多边形的周长无限接近圆的周长,进而来求得较为精确的圆周率(圆周率指圆周长与该圆直径的比率).刘徽计算圆周率是从正六边形开始的,易知圆的内接正六边形可分为六个全等的正三角形,每个三角形的边长均为圆的半径
,此时圆内接正六边形的周长为
,此时若将圆内接正六边形的周长等同于圆的周长,可得圆周率为3,当用正二十四边形内接于圆时,按照上述算法,可得圆周率为__________.(参考数据: 
)
查看答案和解析>>
科目:高中数学 来源:2017届贵州省贵阳市高三2月适应性考试(一)数学理试卷(解析版) 题型:选择题
设
为边长为4的正方形
的边
的中点, 
为正方形区域内任意一点(含边界),则
的最大值为 ( )
A. 32 B. 24 C. 20 D. 16
查看答案和解析>>
科目:高中数学 来源:2017届广西柳州市、钦州市高三第一次模拟考试数学(文)试卷(解析版) 题型:解答题
在四棱锥 中,
中,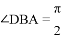 ,
, ,
,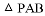 和
和 都是边长为2的等边三角形,设
都是边长为2的等边三角形,设 在底面
在底面 的射影为
的射影为 .
.

(1)求证: 是
是 中点;
中点;
(2)证明: ;
;
(3)求点 到面
到面 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com