练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    在△ABC中,cosA=,tanB=2,求tan(2A+2B)的值.

    解：方法一:在△ABC中,由cosA=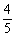,0＜A＜π,得

    sinA=.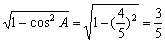

    所以tanA=,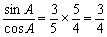

    tanA=,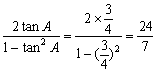

    又tanB=2,

    所以tan2B=.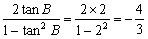

    于是tan(2A+2B)=.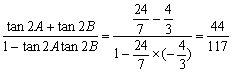

    方法二:在△ABC中,由cosA=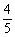,0＜A＜π,得

    sinA=.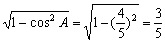

    所以tanA=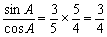.又tanB=2,

    所以tan(A+B)=.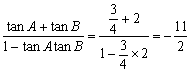

    于是tan(2A+2B)=tan[2(A+B)]

    =.

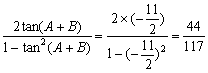    点评：以上两种方法都是对倍角公式、和角公式的联合运用,本质上没有区别,其目的是为了鼓励学生用不同的思路去思考,以拓展学生的视野.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在△ABC中，角A，B，C所对的边分别为a，b，c且满足
    sinA
    cosC
    =
    a
    c
    ．
    （Ⅰ）求角C的大小；
    （Ⅱ）求
    		3
    sinA-cos(B+
    π
    4
    )    的最大值，并求取得最大值时角A的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中，cos(A+C)=-
    3
    5
    ，且a，c的等比中项为
    		35
    ．
    （1）求△ABC的面积；
    （2）若a=7，求角C．

    查看答案和解析>>

    科目：高中数学 来源： 题型：022

    		　　 　　

    在△ABC中, cos(

    　　 　　　　 　　 　　 　　　　 　　 　　 　　　　 　　 　　

    π

    4

    　　

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在△ABC中,cos(+A)=,那么cos2A=____________.

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年人教版高考数学文科二轮专题复习提分训练23练习卷（解析版） 题型：选择题

    在△ABC中, =(cos 18°,cos 72°), =(2cos 63°,2cos 27°),则△ABC面积为(　　)

    (A) (B) (C) (D)

     

    查看答案和解析>>

    同步练习册答案