
分析 (1)利用sin2α+cos2α=1,$\overrightarrow{OC}={sin^2}α\;\;\overrightarrow{OA}+{cos^2}α\;\overrightarrow{OB}$,即可证明C在线段AB上;
(2)由题意,C是AB的中点,由$|\overrightarrow{OA}|=|\overrightarrow{OB}|=1$,且$|\overrightarrow{OA}-\overrightarrow{OB}|=\sqrt{2}$,可得OA⊥OB,即可求$|\overrightarrow{OC}|$.
解答 (1)证明:∵sin2α+cos2α=1,$\overrightarrow{OC}={sin^2}α\;\;\overrightarrow{OA}+{cos^2}α\;\overrightarrow{OB}$,
∴A、B、C共线,且C在线段AB上;
(2)解:由题意,C是AB的中点,
∵$|\overrightarrow{OA}|=|\overrightarrow{OB}|=1$,且$|\overrightarrow{OA}-\overrightarrow{OB}|=\sqrt{2}$,
∴OA⊥OB,
∴$|\overrightarrow{OC}|$=$\frac{1}{2}$|$\overrightarrow{BA}$|=$\frac{\sqrt{2}}{2}$.
点评 本题考查向量知识的运用,考查学生的计算能力,正确运用向量的运算是关键.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 标准差 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2{cos^2}\frac{π}{12}-1$ | B. | $\frac{{2tan{{22.5}°}}}{{1-{{tan}^2}{{22.5}°}}}$ | ||
| C. | 1-2sin275° | D. | sin15°cos15° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
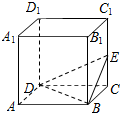
| A. | BD⊥A1C1 | B. | AC1∥平面BDE | ||
| C. | 平面BDE∥平面AB1D1 | D. | 平面A1BD⊥平面BDE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com