练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知函数，关于方程   （为正实数）的根的叙述有下列四个命题 
    ①存在实数，使得方程恰有3个不同的实根；
    ②存在实数，使得方程恰有4个不同的实根；
    ③存在实数，使得方程恰有5个不同的实根；
    ④存在实数，使得方程恰有6个不同的实根；
    其中真命题的个数是（   ）
    A．0B．1C．2D．3
    D
    关于x的方程g[f（x）]-a=0可化为g[f（x）]=a，画出函数y=g[f（x）]和y=a的图象可得解．
    解：关于x的方程g[f（x）]-a=0可化为g[f（x）]=a，
    分别画出函数y=g[f（x）]和y=a（a＞0）的图象，如图．

    由图可知，它们的交点情况是：
    可能有4个、5个、或6个不同的交点，故有：
    ①不存在实数a，使得方程恰有3个不同的实根；
    ②存在实数a，使得方程恰有4个不同的实根；
    ③存在实数a，使得方程恰有5个不同的实根；
    ④存在实数a，使得方程恰有6个不同的实根；
    其中真命题的个数是3．
    故选D．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    给出函数的一条性质：“存在常数，使得对于定义域中的一切实数均成立”，则下列函数中具有这条性质的函数是（   ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题


    （本题满分12分）
    已知函数 .
    （1）若在上是增函数, 求实数a的取值范围.
    （2）若是的极大值点,求在上的最大值；
    （3）在（2）的条件下，是否存在实数b，使得函数的图像与函数的图像恰有3个交点，若存在，求出b的取值范围，若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    函数的图像恒过定点A，若点A在直线，上，则的最小值是   ▲  ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    设函数f(x)＝a1＋a2x＋a3x2＋…＋anxn－1，f(0)＝，数列{an}满足f(1)＝n2an(n∈N*)，则数列{an}的通项an＝_______________

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知，，则（  ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    在一个特定的时间段内，以点为中心的海里以内的海域被设为警戒水域，点正北55海里处有一雷达观测站，某时刻测得一艘匀速直线行驶的船只位于点北偏东且与点相距海里的位置，经过40分钟又测得该船已经驶到点北偏东（其中且与点相距海里的处.
     求该船的行驶速度；
     若该船不改变航行方向继续行驶，判断它是否会进入警戒线水域，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    已知偶函数在区间上单调递增，且满足，给出下列判断：（1）；（2）在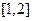上是减函数；（3）的图像关于直线对称；（4）函数在处取得最大值；（5）函数没有最小值，其中正确的序号是              。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    设，则="              " ；

    查看答案和解析>>

    同步练习册答案