
【题目】直线1通过点P(1,3)且与两坐标轴的正半轴交于A、B两点.
(1)直线1与两坐标轴所围成的三角形面积为6,求直线1的方程;
(2)求OA+OB的最小值;
(3)求PAPB的最小值.
【答案】
(1)解:设直线l的方程为y﹣3=k(x﹣1)(k<0),
由x=0,得y=3﹣k,由y=0,得x= ![]() ,
,
∴ ![]() =6,解得:k=﹣3
=6,解得:k=﹣3
(2)解:OA+OB=3﹣k+1﹣ ![]() =4+(﹣k)+(﹣
=4+(﹣k)+(﹣ ![]() )
) 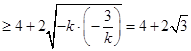 .
.
当且仅当﹣k=﹣ ![]() ,即k=﹣
,即k=﹣ ![]() 时上式“=”成立
时上式“=”成立
(3)解:设直线l的倾斜角为α,则它的方程为 ![]() (t为参数),
(t为参数),
由A、B是坐标轴上的点,不妨设yA=0,xB=0,
∴0=3+tsinα,即PA=|t|= ![]() ,
,
0=3+tcosα,即PB=|t|=﹣ ![]() .
.
故PAPB= ![]() =﹣
=﹣ ![]() .∵90°<α<180°,
.∵90°<α<180°,
∴当2α=270°,即α=135°时,PAPB有最小值.
∴直线方程为  (t为参数),化为普通方程即x+y﹣4=0
(t为参数),化为普通方程即x+y﹣4=0
【解析】(1)设出直线l的方程为y﹣3=k(x﹣1)(k<0),求出直线在两坐标轴上的截距,代入三角形面积公式得答案;(2)写出OA+OB的含有k的代数式,利用基本不等式求得最值;(3)设出直线l的参数方程,利用t的几何意义求出PA,PB然后利用三角函数求最值.
【考点精析】关于本题考查的截距式方程,需要了解直线的截距式方程:已知直线![]() 与
与![]() 轴的交点为A
轴的交点为A![]() ,与
,与![]() 轴的交点为B
轴的交点为B![]() ,其中
,其中![]() 才能得出正确答案.
才能得出正确答案.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】要在墙上开一个上部为半圆,下部为矩形的窗户(如图所示),在窗框总长度为l的条件下, 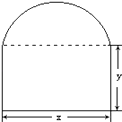
(1)请写出窗户的面积S与圆的直径x的函数关系;
(2)要使窗户透光面积最大,窗户应具有怎样的尺寸?并写出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c(a,b,c∈R且a≠0),若对任意实数x,不等式2x≤f(x) ![]() (x+1)2恒成立.
(x+1)2恒成立.
(1)求f(1)的值;
(2)求a的取值范围;
(3)若函数g(x)=f(x)+2a|x﹣1|,x∈[﹣2,2]的最小值为﹣1,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,任取
,任取![]() ,定义集合:
,定义集合:
![]() ,点
,点![]() ,
, ![]() 满足
满足![]() .
.
设![]() 分别表示集合
分别表示集合![]() 中元素的最大值和最小值,记
中元素的最大值和最小值,记![]() .则
.则
(1) 若函数![]() ,则
,则![]() =______;
=______;
(2)若函数![]() ,则
,则![]() 的最小正周期为______.
的最小正周期为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于集合![]() ,定义函数
,定义函数![]() 对于两个集合
对于两个集合![]() ,定义集合
,定义集合![]() . 已知
. 已知![]() ,
, ![]() .
.
(Ⅰ)写出![]() 和
和![]() 的值,并用列举法写出集合
的值,并用列举法写出集合![]() ;
;
(Ⅱ)用![]() 表示有限集合
表示有限集合![]() 所含元素的个数,求
所含元素的个数,求![]() 的最小值;
的最小值;
(Ⅲ)有多少个集合对![]() ,满足
,满足![]() ,且
,且![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2x﹣2﹣a(a≤0),
(1)若a=﹣1,求函数的零点;
(2)若函数在区间(0,1]上恰有一个零点,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=alnx+x2(a为实常数).
(1)当a=﹣4时,求函数f(x)在[1,e]上的最大值及相应的x值;
(2)当x∈[1,e]时,讨论方程f(x)=0根的个数.
(3)若a>0,且对任意的x1 , x2∈[1,e],都有 ![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(x1 , f(x1)),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣ ![]() <φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣
<φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣ ![]() ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为
),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为 ![]()
(1)求函数f(x)的解析式;
(2)若方程3[f(x)]2﹣f(x)+m=0在x∈( ![]() ,
, ![]() )内有两个不同的解,求实数m的取值范围.
)内有两个不同的解,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com