Question

方程（x²⁰⁰⁶+1）（1+x²+x⁴+…+x²⁰⁰⁴）=2006x²⁰⁰⁵的实数解的个数为    ．

Answer 1

【答案】分析：将方程等价变形，利用基本不等式，结合等号成立的条件，即可求得结论．
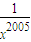
解答：解：（x²⁰⁰⁶+1）（1+x²+x⁴+…+x²⁰⁰⁴）=2006x²⁰⁰⁵，等价于（x+）（1+x²+x⁴+…+x²⁰⁰⁴）=2006
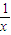
等价于x+x³+x⁵+…+x²⁰⁰⁵++++…+=2006，故x＞0，否则左边＜0．
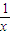
所以2006=x++x³++…+x²⁰⁰⁵+≥2×1003=2006．
等号当且仅当x=1时成立．
所以x=1是原方程的全部解．
因此原方程的实数解个数为1
故答案为1．
点评：本题考查函数与方程思想，考查基本不等式的运用，考查学生分析解决问题的能力，属于中档题．