
【题目】下列说法中错误的个数是( )
①若直线![]() 平面
平面![]() ,直线
,直线![]() ,则
,则![]() ;②若直线l和平面
;②若直线l和平面![]() 内的无数条直线垂直,则直线l与平面
内的无数条直线垂直,则直线l与平面![]() 必相交;③过平面
必相交;③过平面![]() 外一点有且只有一条直线和平面
外一点有且只有一条直线和平面![]() 垂直;④过直线
垂直;④过直线![]() 外一点有且只有一个平面和直线a垂直
外一点有且只有一个平面和直线a垂直
A.0B.1C.2D.3
【答案】C
【解析】
由线面平行,线面垂直的判定以及其几何性质特征对四个命题一一判断即可得出答案.
①错误.若直线![]() 平面α,直线
平面α,直线![]() ,则l与α平行、相交或l在α内、
,则l与α平行、相交或l在α内、![]() 都有可能;
都有可能;
②错误.若直线l和平面α内的无数条直线垂直,则直线l与平面α平行、相交或l在α内都有可能;
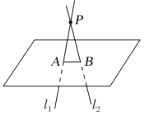
③正确.如图,假如![]() 与
与![]() 都过点P,且都与平面α垂直,由直线与异面垂直的性质定理可知
都过点P,且都与平面α垂直,由直线与异面垂直的性质定理可知![]() ,这与
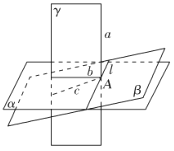
,这与![]() 矛盾,故正确;④正确.不论点A是否在直线a上(如图),设过点A与直线a垂直的平面为α.如果还有一个平面β过点A与直线a垂直,且
矛盾,故正确;④正确.不论点A是否在直线a上(如图),设过点A与直线a垂直的平面为α.如果还有一个平面β过点A与直线a垂直,且![]() ,设过点A和直线a且不过l的平面为γ,且
,设过点A和直线a且不过l的平面为γ,且![]() ,
,![]() .因为
.因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,这样在同一平面γ内,过一点A就有两条直线b,c都与a垂直,这是不可能的.所以,过点A和直线a垂直的平面只有一个.
,这样在同一平面γ内,过一点A就有两条直线b,c都与a垂直,这是不可能的.所以,过点A和直线a垂直的平面只有一个.
故选:C.


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
【题目】如图,已知点P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点.

(1)求证:MN∥平面PAD;
(2)在PB上确定一个点Q,使平面MNQ∥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() .已知点
.已知点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在
在![]() 上,
上,![]() 是边长为4的等边三角形.
是边长为4的等边三角形.
(1)求![]() 的值;
的值;
(2)若直线![]() 是过定点
是过定点![]() 的一条直线,且与抛物线
的一条直线,且与抛物线![]() 交于
交于![]() 两点,过
两点,过![]() 作
作![]() 的垂
的垂
线与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
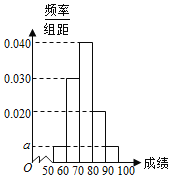
【题目】某职称晋级评定机构对参加某次专业技术考试的100人的成绩进行了统计,绘制了频率分布直方图![]() 如图所示
如图所示![]() ,规定80分及以上者晋级成功,否则晋级失败.
,规定80分及以上者晋级成功,否则晋级失败.
晋级成功 | 晋级失败 | 合计 | |
男 | 16 | ||
女 | 50 | ||
合计 |
![]() Ⅰ
Ⅰ![]() 求图中a的值;
求图中a的值;
![]() Ⅱ
Ⅱ![]() 根据已知条件完成下面
根据已知条件完成下面![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为“晋级成功”与性别有关?
的把握认为“晋级成功”与性别有关?
![]() Ⅲ
Ⅲ![]() 将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的数学期望
将频率视为概率,从本次考试的所有人员中,随机抽取4人进行约谈,记这4人中晋级失败的人数为X,求X的数学期望![]() 与方差
与方差![]() .
.
![]() 参考公式:
参考公式:![]() ,其中
,其中![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域是
的定义域是![]() ,对任意
,对任意![]() ,当
,当![]() 时,
时,![]() .关于函数
.关于函数![]() 给出下列四个命题:①函数
给出下列四个命题:①函数![]() 是周期函数;②函数
是周期函数;②函数![]() 是奇函数;③函数
是奇函数;③函数![]() 的全部零点为
的全部零点为![]() ;④当
;④当![]() 时,函数
时,函数![]() 的图象与函数
的图象与函数![]() 的图象有且只有三个公共点.其中真命题的序号为__________.
的图象有且只有三个公共点.其中真命题的序号为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中:
①定义在R上的函数f(x)在区间(-∞,0]上是增函数,在区间[0,+∞)上也是增函数,则函数f(x)在R上是增函数;②若f(2)=f(-2),则函数f(x)不是奇函数;③函数y=x-0.5是(0,1)上的减函数;④对应法则和值域相同的函数的定义域也相同;⑤若x0是二次函数y=f(x)的零点,且m<x0<n,那么f(m)f(n)<0一定成立.
写出上述所有正确结论的序号:_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com