
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)令g(x)=f(x)+ax,只要g(x)在(0,+∞)上为增函数,求出函数的导数,得到关于a的不等式,解出即可;
(3)分别表示出h(x1),h(x2)两式相减,得到$a=\frac{{2ln\frac{x_2}{x_1}}}{{{x_2}-{x_1}}}-({x_2}+{x_1})$,令$t=\frac{x_2}{x_1}∈(1,4),φ(t)=lnt-\frac{3t-3}{t+2}$,根据函数的单调性证明即可.
解答 解:(1)f(x)的定义域为(0,+∞),
${f^'}(x)=x-(a+1)+2(a-1)\frac{1}{x}=\frac{{{x^2}-(a+1)x+2(a-1)}}{x}=\frac{{(x-2)[{x-(a-1)}]}}{x}$,
①若a-1=2,则a=3,${f^'}(x)=\frac{{{{(x-2)}^2}}}{x}>0$,f(x)在(0,+∞)上单调递增;
②若a-1<2,则a<3,而a>1,∴1<a<3,
当x∈(a-1,2)时,f′(x)<0;当x∈(0,a-1)及(2,+∞)时f′(x)>0,
所以f(x)在(a-1,2)上单调递减,在(0,a-1)及(2,+∞)单调递增;
③若a-1>2,则a>3,同理可得f(x)在(2,a-1)上单调递减,在(0,2)及(a-1,+∞)单调递增.
(2)假设存在a,对任意x1,x2∈(0,+∞),x1≠x2,有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}+a>0$恒成立,
不妨设0<x1<x2,只要$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}+a>0$,即f(x2)+ax2>f(x1)+ax1,
令g(x)=f(x)+ax,只要g(x)在(0,+∞)上为增函数,
$g(x)=\frac{1}{2}{x^2}-x+2(a-1)lnx$${g^'}(x)=x-1+\frac{2(a-1)}{x}=\frac{{{x^2}-x+2(a-1)}}{x}=\frac{{{{(x-\frac{1}{2})}^2}+2a-\frac{9}{4}}}{x}$,
只要g′(x)≥0在(0,+∞)恒成立,只要$2a-\frac{9}{4}≥0,a≥\frac{9}{8}$,
故存在$a∈[{\frac{9}{8},+∞})$时,对任意x1,x2∈(0,+∞),x1≠x2,有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}+a>0$恒成立.
(3)证明:由题意知,$h(x)=[\frac{1}{2}{x^2}-(a+1)x+2(a-1)lnx]+[-\frac{3}{2}{x^2}+x+(4-2a)lnx]=2lnx-{x^2}-ax$,
$h({x_1})=2ln{x_1}-x_1^2-a{x_1}=0,h({x_2})=2ln{x_2}-x_2^2-a{x_2}=0$
两式相减,整理得$2ln\frac{x_2}{x_1}+({x_1}-{x_2})({x_1}+{x_2})=a({x_2}-{x_1})$,
所以$a=\frac{{2ln\frac{x_2}{x_1}}}{{{x_2}-{x_1}}}-({x_2}+{x_1})$,又因为$h'(x)=\frac{2}{x}-2x-a$,
所以$h'(\frac{{2{x_1}+{x_2}}}{3})=\frac{6}{{2{x_1}+{x_2}}}-\frac{2}{3}(2{x_1}+{x_2})-a=-\frac{2}{{{x_2}-{x_1}}}[ln\frac{x_2}{x_1}-\frac{{3\frac{x_2}{x_1}-3}}{{2+\frac{x_2}{x_1}}}]-\frac{1}{3}({x_1}-{x_2})$,
令$t=\frac{x_2}{x_1}∈(1,4),φ(t)=lnt-\frac{3t-3}{t+2}$,则${φ^'}(t)=\frac{(t-1)(t-4)}{{t{{(t+2)}^2}}}<0$,
所以φ(t)在(1,4)上单调递减,故φ(t)<φ(1)=0,
又$-\frac{2}{{{x_2}-{x_1}}}<0,-\frac{1}{3}({x_1}-{x_2})>0$,所以$h'(\frac{{2{x_1}+{x_2}}}{3})>0$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想、分类讨论思想,是一道综合题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,2) | B. | (-1,2) | C. | [1,2) | D. | [-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
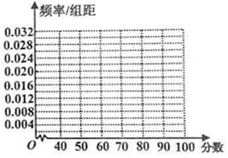 学校从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),得到如下数学成绩的频率分布表:
学校从参加高三年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),得到如下数学成绩的频率分布表:| 分组 | 频数 | 频率 |
| [40,50) | 2 | |
| [50,60) | 3 | |
| [60,70) | 0.28 | |
| [70,80) | 15 | |
| [80,90) | 12 | |
| [90,100] | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com